Theorem of Pythagoras With Applications

The so-called Theorem of Pythagoras states that for a right triangle, it is always true that

c ² = a ² + b ²

Recall that in a right triangle, the longest side, opposite the right angle, is called the hypotenuse. Thus the Theorem of Pythagoras states that for right triangles

the square of the length of the hypotenuse = the sum of the squares of the lengths of the other two (shorter) sides

If the lengths of any two sides of a right triangle are known, then the length of the remaining third side can be computed using this formula.

(In the examples that follow, we will observe the convention that for right triangles, the right angle is always labelled C, and the other two angles are labelled A and B. The labels for the sides are the lower-case characters of the angles opposite. So, the side opposite the right angle vertex is always labelled c, the side opposite vertex A is always labelled a, and the side opposite vertex B is always labelled b. These symbols are somewhat loosely used simply as names of these parts of the triangle, and as well, in formulas, they represent the sizes of the parts. Thus b is a label for the side opposite vertex B, but in a formula, the symbol b stands for the length of that side. Similarly, the symbol B is a label for a vertex, but also, in formulas represents the size of the angle at the vertex, in some appropriate unit of measurement such as degrees.)

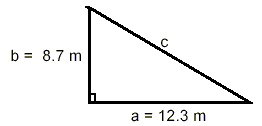
Example 1:

The two perpendicular sides of a right triangle have lengths 12.3 m and 8.7 m, respectively. Compute the length of the hypotenuse of this right triangle.

solution:

The situation is shown in the sketch to the right. We are asked to determine the value of c. Applying Pythagoras’s Theorem directly gives

c ² = a ² + b ²

= (12.3 m) ² + (8.7 m) ²

= 226.98 m ²

Therefore,

Since the original measurements are rounded to one decimal place, we should probably do so with our answer. Thus, the length of the hypotenuse of this right triangle is 15.1 m.

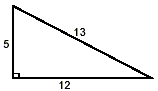
Caution:

People are sometimes tempted to apply Pythagoras’s Theorem even when the triangle in question is either not a right triangle or is not known for sure to be a right triangle. Pythagoras’s Theorem only works for right triangles. If it is applied in any way to triangles which are not right triangles, it is sure to give erroneous results.

If we know the lengths of the three sides of a triangle, Pythagoras’s Theorem can also be used to determine whether or not that triangle is a right triangle.

Example 2:

Each of the following sets of three numbers are claimed to be lengths of sides of right triangles. Confirm that this is true in each case.

(i) 8, 19, 13

(ii) 13, 12, 5

(iii) 7, 42, 9

solution:

In each case, the longest side must be the hypotenuse (since the hypotenuse is always the longest side of a right triangle). If the given triangle is really a right triangle, then the square of the length of the longest side must be exactly equal to the sum of the squares of the lengths of the other two sides.

So, for case (i), the length 19 must be the length of the hypotenuse. Here

19 ² = 361.

But

8 ² + 13 ² = 64 + 169 = 233.

Since 233 361, these three numbers do not satisfy Pythagoras’s Theorem, and so they cannot represent the lengths of the three sides of a right triangle.

For case (ii), the length 13 must be the length of the hypotenuse. Then

13 ² = 169

and

5 ² + 12 ² = 25 + 144 = 169

Since these two results are equal, we conclude that these three lengths do form a right triangle, as sketched in the figure.

For case (iii), the length 42 would have to be the length of the hypotenuse. Then, checking, we find that

42 ² = 1764

and

7 ² + 9 ² = 49 + 81 = 130

Since 1764 130, we know that these three lengths cannot form a right triangle. In fact, since 42 is greater than 7 + 9 = 16, it turns out that these three lengths cannot even form a triangle of any shape!