|
Tuesday 21st of January |
Solving Linear EquationsIntroductionAn equation is a statement that two mathematical expressions are equal. 2x + 4 = 8 is an equation. To solve an equation involving x means you are trying to find all the values of x that make the equation true. The solution set is the set of all real numbers that are solutions to the equation. If every real number solves an equation, the equation is called an identity. For example, 2(x- 1) = 2x - 2 is an identity equation because any real number you substitute for x makes this equation true. If only specific real numbers solve an equation, the equation is called a conditional equation. For example, x + 4 = 6 is true if and only if x = 2 so it is a conditional equation. An equation that has no solution is said to have an empty set
solution. For example, You check a solution set by merely substituting your answer in the original equation to verify your results. Example: Solve x + 4 = 6 Answer x = 2 To check: Substitute 2 everywhere you have an x.
Trial SolutionsSee if 5 satisfies the equation 2x + 3 = 10 To check 5 in the equation, substitute it wherever you have an x. 2x + 3 = 10 Original equation
So 5 is not a solution to this equation!!!! Two equations that have the same solution set are called equivalent equations. To solve linear equations, you are trying to work your way to the simple equation x = ______
A linear equation in one variable x is an equation that can be written in the standard form ax + b = c. It is called a first-degree equation because its variable has an exponent of 1. A linear equation should always have exactly one solution. ExamplesSolve the following standard linear equation for x and check your answer by substitution.
CHECK: Substitute 3 for each x in the original equation
|
|


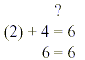 And the solution checks out fine!
And the solution checks out fine! 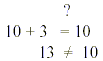
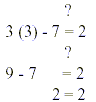 and the solution checks !!!
and the solution checks !!!