Factoring Trinomials
A polynomial that has no greatest common factor (otherthan 1)
may still be factorable. For example, the polynomial x +5x+6
can be factored as (x+2)(x+3). To see that this is correct, find
the product (x+2)(x+3); you should get x+5x+6.
A polynomial such as this with three terms is called a trinomial.
To factor the trinomial x+5x+6
where thecoefficient of is 1, we use FOIL backwards.
EXAMPLE
Factor y+8y+5
Solution
Since the coefficient of y
is 1, factor by finding two numbers whose product is 15 and whose
sum is 8. Since the constant and the middle term arepositive, the
numbers must both be positive. Begin by listing all pairs of
positiveintegers having a product of 15. As you do this, also
form the sum of each pairof numbers.
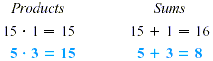
The numbers 5 and 3 have a product of 15 and a sum of 8. Thus,
y+8y+5 factors as
y+8y+5 = (y+5)(y+3)
The answer also can be written as (y+5)(y+3)
If the coefficient of the squared term is not 1, work as shown
below.
EXAMPLE
Factor 2x+9xy-5y.
Solution
The factors of 2x
are 2x and x; the possible factors of -5y
are -5y and y, or 5y and -y. Try various combinations of these
factors until one works (if, indeed,any work). For example, try
the product (2x + 5y)(x-y).
(2x + 5y)(x-y) = 2x-2xy+5xy-5y
= 2x+3xy-5y
This product is not correct, so try another combination.
(2x - y)(x+5y) = 2x+10xy-xy-5y
= 2x+9xy-5y
Since this combination gives the correct polynomial,
2x+9xy-5y = (2x - y)(x+5y)
|
