Least Common Multiples
To add fractions, we need to change the denominators to the least common multiple.
In a multiplication problem, the product (result of multiplication) is also called a multiple
of the numbers or factors.
Example:
What is the least common multiple of 6 and 9?
Multiples of 6 are: 6, 12, 18, 24, 30, 36, 42,
48, 54, ...
Multiples of 9 are: 9, 18, 27, 36, 45, 54,
63, ...
The numbers in bold are common multiples of 6 and 9.
The least (or lowest or smallest) common multiple of 6 and 9 is 18.
- We do not call “zero†a multiple of any other number! So the least common multiple
of two numbers is never 0. The product is zero if any of the factors are zero.
- The letters LCM are often used for the term Least Common Multiple.
Example:
What is the least common multiple of 12 and 24?
Multiples of 12 are: 12, 24, 36, 48, 60, 72, …
Multiples of 24 are: 24, 48, 72, …
The answer is easy of one number is a multiple of another.
The least common multiple is 24.
Do any two numbers always have a common multiple? Yes. The product of the numbers
is a common multiple. It may or may not be the least common multiple.
By the way, if two numbers are both prime, then their product is always the least common
multiple.
To add or subtract fractions, we need to change them so they have common
denominators. Any common multiple will work, but the least common multiple will give
you the smallest (and easiest) numbers to work with.
Example:
Change this problem to use the least common denominator:
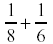
Multiples of 6 are: 6, 12, 18, 24
Multiples of 8 are: 8, 16, 24
The least common multiple is 24, so now convert the fractions.
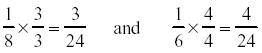
Answer:
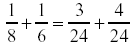
|