The Distance Formula
The distance between any two points in the xy-plane can be found using
the distance formula.
Formula
The Distance Formula
Let (x1, y1) and (x2, y2) represent any two points in the xy-plane. The
distance, d, between the points is given by
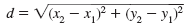
If the points lie on a horizontal line, then this simplifies to d = | x2
- x1 |.
If the points lie on a vertical line, then this simplifies to d = |y2
- y1|.
Note:In the distance formula, it doesn’t matter
which point is considered (x1, y1) or (x2, y2). The resulting distance is the same.
Example 1
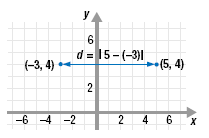
Find the distance between (-3, 4) and (5, 4).
Solution
Since the points (-3, 4) and (5, 4) have the same
y-coordinate, 4, they lie on a horizontal line.
| So, we use the formula:
Let x1 =-3 and x2 = 5.
Simplify.
Find the absolute value.
The distance between (-3, 4) and (5, 4) is 8 units. |
d = | x2
- x1 | d = | 5 - (-3) |
d = | 8 |
d = 8
|
 |
In the formula, d = | x2
- x1 |, it doesn’t
matter which x-coordinate is assigned to
x1 and which is assigned to x2. The
resulting distance is the same.
That is:
|5 - (-3)| = |-3 - 5|
|8| = |-8|
8 = 8
Example 2
Find the distance between (-3, 8) and (5, -1).
Solution
| The points do not lie on a horizontal or vertical line. |
|
| Therefore, use the distance formula. |
 |
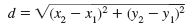| Let (x1, y1) = (-3, 8) and (x2, y2)
= (5, -1). |
|
| Substitute. |
 |
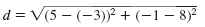| Simplify. |
 |
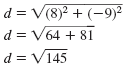The distance between the points (-3, 8) and (5, -1) i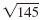s
 units.
Note:
If we switch the points and let
(x1, y1) = (5, -1) and
(x2, y2) = (-3, 8), we get the
same answer.
We can use a calculator to
approximate
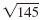≈ 12.04.
|
