Properties of Exponents
The table below lists several properties of exponents. Here, m and n are
real numbers.
| Name
|
Property |
Example |
| Multiplication Property |
xm · xm
= x m + n |
54 · 52
= x 4 + 2 = 56 |
| Division Property |
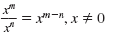 |
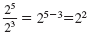 |
| Power of a Power
Property |
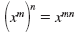 |
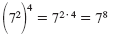 |
| Power of a Product
Property |
(xy)n = xn yn |
(2x)3 = 23 x3 = 8x3 |
| Power of a Quotient Property |
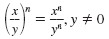 |
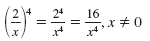 |
| Zero Power Property |
x0 = 1, x ≠ 0 |
170 = 1 |
| Negative Exponent |
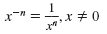 |
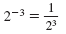 |
Example 1
Simplify: 2xy4(3x5y)(x3y5)2
| We can drop parentheses around the
quantity (3x5y) since it has an exponent
of 1. |
Solution |
2xy4(3x5y)(x3y5)2 |
| That is, (3x5y) = (3x5y)1
= 3x5y. |
Use the Power of a Product Property.
|
= 2xy4(3x5y)(x3·2y5·2) |
| |
Simplify.
|
= 2xy4(3x5y)(x6y10)
= 2xy4 · 3x5y
· x6y10 |
| Recall: x = x1 and y = y1 |
Multiply the constants, 2 and 3. |
= 6xy4 · x5y
· x6y10 |
| |
Use the Multiplication Property of Exponents.
|
= 6x1+5+6 y4+1+10 |
| So, 6xy4 = 6x1y4 and x5y
= x5y1. |
Simplify. |
= 6x12 y15 |
| |
So, the result is 6x12y15. |
|
|