Multiplying Mixed Numbers
Some situations require us to multiply mixed numbers. For
instance, suppose that your regular hourly wage is 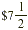 and that you make time-and-a-half for working
overtime. To find your overtime hourly wage, you need to multiply and that you make time-and-a-half for working
overtime. To find your overtime hourly wage, you need to multiply
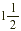 by by 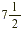 . The key here is to first rewrite each mixed number
as an improper fraction. . The key here is to first rewrite each mixed number
as an improper fraction.
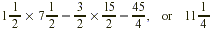
So you make 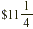 per hour overtime. per hour overtime.
To Multiply Mixed Numbers
- change each mixed number to its equivalent improper
fraction,
- follow the steps for multiplying fractions, and
- write the answer in simplest form.
EXAMPLE 1
Multiply by 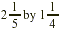 . .
Solution
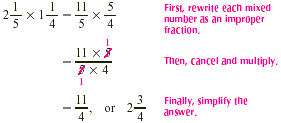
EXAMPLE 2
Multiply: 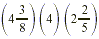
Solution
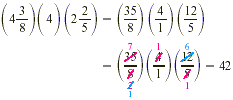
Note in this problem that, although there are several ways to
cancel, the answer always comes out the same.
EXAMPLE 3
A nurse gave a patient 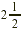 tablets of the medication atropine sulfate. If each
tablet contains tablets of the medication atropine sulfate. If each
tablet contains 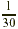 grain (gr) of this medication, how much atropine
sulfate did the patient receive? grain (gr) of this medication, how much atropine
sulfate did the patient receive?
Solution
To find the total amount of atropine sulfate administered, we
need to multiply 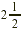 by by 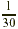 . .
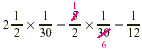
Therefore the nurse gave the patient 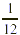 gr of atropine sulfate. gr of atropine sulfate.
EXAMPLE 4
A lawn surrounding a garden is to be installed, as depicted in
the following drawing.

How many square yards of turf will we need to cover the lawn?
Solution
Let’s break this problem into three steps. First, we find
the area of the rectangle with dimensions 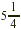 yards and yards and 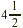 yards. Then, we find the area of the small rectangle
whose length and width are yards. Then, we find the area of the small rectangle
whose length and width are 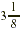 yards and 2 yards, respectively. Finally, we
subtract the area of the small rectangle from the area of the
large rectangle. yards and 2 yards, respectively. Finally, we
subtract the area of the small rectangle from the area of the
large rectangle.
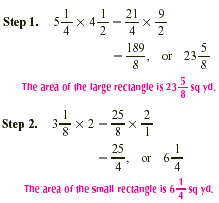
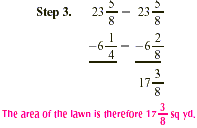
We will need 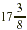 sq yd of turf for the lawn. sq yd of turf for the lawn.
|