Solving Linear Equations
Definitions
An equation is formed when two expressions are linked by an equals sign.
For example:
7(x - 2) = 3x - 9 + 5x
To solve an equation means to find the values of the variable that make the
equation a true statement. Those values are called the solution of the
equation.
For example, x = -5 is the solution of
7(x - 2) = 3x - 9 + 5x . When we
replace x with -5 and simplify, the result is a true statement.
| Original equation.
|
7(x - 2) = |
3x |
- 9 + 5x |
| Replace x with -5.
|
7(-5 - 2) = |
3(-5) |
- 9 + 5(-5) |
| Simplify.
|
7(-7) = |
- 15 |
- 9 - 25 |
| The result is a true statement. |
- 49 = |
- 49 |
|
A linear equation in one variable is an equation that can be written in the
form
ax + b = 0 where a and b are real numbers, and a ≠ 0.
Note:
The equation ax + b = 0 is a linear
equation because the exponent of the
variable, x, is 1.
Solving a Linear Equation
To find the solution of a linear equation, isolate the variable. That is, use
algebraic operations to get the variable by itself on one side of the equals
sign.
Here is the procedure to solve a linear equation.
Procedure
To Solve a Linear Equation
Step 1 Remove any parentheses using the Distributive Property.
Step 2 On each side of the equation, combine like terms.
Step 3 Isolate the variable.
Step 4 Check the solution in the original equation.
Note:
The distributive property states
that for all real numbers, a, b, c:
a(b + c) = ab + ac
Example 1
Solve: 3x + 7 - 8x = -13
Solution
|
Step 1 Remove parentheses.
There are no parentheses to remove.
|
|
|
| Step 2 On each side of the equation,
combine like terms.
Combine 3x and -8x.
|
-5x + 7 - 8x
-5x + 7 |
= -13 = -13 |
| Step 3 Isolate the variable. |
|
|
| Subtract 7 from both sides.
Simplify.
Divide both sides by -5. |
-5x + 7 - 7 -5x
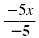
x |
= -13 - 7 = -20
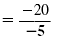
= 4 |
| Step 4 Check the solution in the original equation.
x = 4 is a solution if it makes the equation true. |
|
|
| Is Is
Is |
3x + 7
3(4) + 7
12 + 7
|
- 8x - 8(4)
- 32
- 13 |
= -13 = -13 ?
= -13 ?
= -13 ? Yes |
The solution is x = 4.
|