Square Roots
Some quadratic equations can be readily solved using square roots.
Before we look at some examples, it will be helpful to review what
we have learned about square roots.
• Recall that every positive number has two square roots.
For example:
The positive square root of 25, written
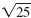 , is
+5 since
(+5)2 = 25. , is
+5 since
(+5)2 = 25.
The negative square root of 25, written -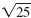 , is
-5 since
(-5)2 = 25. , is
-5 since
(-5)2 = 25.
• A square root is in simplified form when there are:
• No perfect square factors under a square root symbol.
• No fractions under a square root symbol.
• No square roots in the denominator of a fraction.
• The Multiplication Property of Square Roots states that the square root
of a product is the product of the square roots. That is, if a and b are
nonnegative real numbers, then
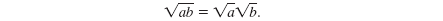
We can use this property to simplify a square root.
For example, let’s simplify
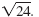 |
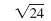 |
| Write 24 as a product. |
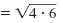 |
| Use the Multiplication Property of Square Roots.
|
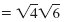 |
Simplify
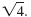 |
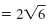 |
• The Division Property of Square Roots states that the square root of a
quotient is the quotient of the square roots. That is, if a and b are
nonnegative real numbers and b ≠ 0, then

For example, let’s simplify
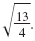 |
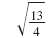 |
| Use the Division Property of Square Roots.
|
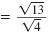 |
Simplify
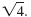 |
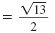 |
|