Composition of Functions
Example 1
The graphs of f(x) and g(x) are shown. Use these graphs to find (g
○ f)(3).
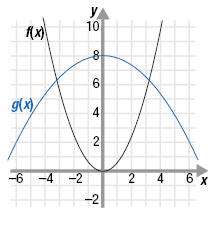
Solution
Since (g ○ f)(3) = g[f(3)], we first must find f(3). On the graph, locate f(3).
That is, find the y-value of f when x = 3.
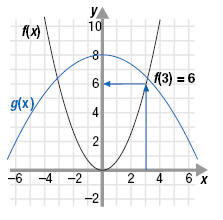
From the graph, we see that when x = 3, y = 6. Thus, f(3) = 6.
Now, use 6 as the input for g(x). That is, find g(6). To do this, find the
y-value of g when x = 6.
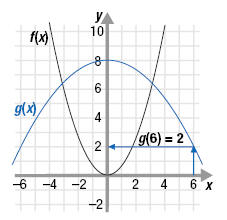
From the graph we see that when x = 6, y = 2. Therefore, (g
○ f)(3) = 2.
Example 2
Graph the function f(x) = x2 - 2. If g(x) = |x|, sketch the graph of
(g ○ f)(x).
Solution
The graph of f(x) = x2 - 2 is the same as the graph of f(x) = x2 but shifted
down 2 units.
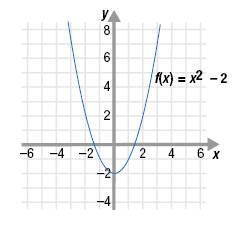
| Now, find (g ○ f)(x).
Replace f(x) with x2 - 2.
In g(x), replace x with x2 - 2. |
(g ○ f)(x) |
= g[f(x)] = g[x2 - 2]
= | x2 - 2 | |
The graph of g(x) = | x2 - 2 | is the same as f(x) = x2
- 2 except that all
outputs are nonnegative because of the absolute value symbols.
To graph (g ○ f)(x) = | x2
- 2 |, we can reflect across the x-axis the part of
the graph of f(x) = x2 - 2 that is below the x-axis.
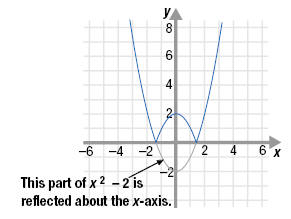
The graph of (g ○ f)(x) = | x2
- 2 | lies on and above the x-axis.
|