Multiplying and Dividing Fractions
Multiplying one algebraic fraction by another algebraic
fraction, or dividing one algebraic fraction by another algebraic
fraction, brings together three topics with which you are already
familiar:
(i) the basic formalism:
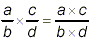
and
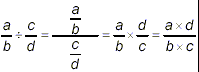
(ii) the methods of simplifying fractions by cancellation of
factors common to the numerator and denominator
and
(iii) using the laws of exponents when the factors being
multiplied or divided are powers:
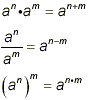
These laws of exponents imply, among other things, that we can
move factors from the numerator to the denominator or the
reverse, as long as we change the sign of the exponent at the
same time. This property can make cancellations involving powers
of a specific symbol very easy. For instance, we can do
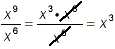
or
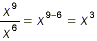
or even
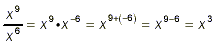
The rest of this document consists of a collection of examples
illustrating how these three sets of properties can be used to
carry out multiplication and division with algebraic fractions,
ensuring that the final result is in simplest possible form.
Example 1: Simplify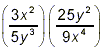 . .
solution: Writing the two sets of brackets next to each other
in this fashion indicates that the two fractions are to be
multiplied. So
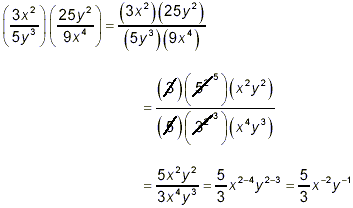
This result is technically correct, but many people view
negative exponents as unattractive and somewhat conducive to
misunderstanding or misinterpretation. Most practitioners would
recommend writing the final answer here in the form of a proper
fraction containing no negative exponents. Thus, the best way to
state the final answer is
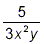
|