Complex Numbers
Real numbers and imaginary numbers are each examples of complex
numbers.
For example, we can combine the real number 5 and the imaginary
number 4i to form the complex number, 5 + 4i.
Definition —
Complex Number
A complex number is a number that can be written in the form a + bi, where a and b are real numbers and
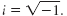
• The real number a is called the real part of the complex number.
• The real number b is called the imaginary part of the complex
number.
Note:
- In the complex number a + bi, the
imaginary part is b, not bi.
- In a complex number a + bi, a and b can
be any real numbers, including zero.
Here are some examples of complex numbers:
| Complex Number
a + bi
-8 + 12i
15 - 7i
6 + 0i
0 - 2i
|
Real Part
a
-8
15
6
0 |
Imaginary Part
b
12
-7
0
-2 |
A complex number whose imaginary part, b, is 0, is called a real number.
For example, the complex number 6 + 0i can be written as 6.
The number 6 is a real number.
This means that the real numbers are a subset of the complex numbers.
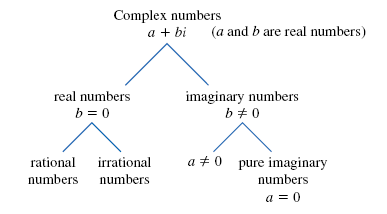
All real numbers are complex numbers of the form a + 0i.
Note:
All real numbers are complex numbers.
However, not all complex numbers are
real numbers.
A complex number whose imaginary part, b, is not 0, is called an imaginary number.
For example, the complex number 6 + 4i is an imaginary number.
The imaginary numbers are a subset of the complex numbers.
A complex number whose real part, a, is 0, is called a pure imaginary
number.
For example, the complex number 0 - 2i can be written as -2i. The number -2i is a pure imaginary number.
Next we will study the arithmetic of complex numbers. That is, we will
learn how to add, subtract, multiply, and divide them.
Before we do so, it will be helpful to define what it means for one
complex number to be equal to another complex number.
Definition — Equality of Complex Numbers
Two complex numbers are equal if their real parts are equal and
their imaginary parts are equal.
That is, a + bi = c + di if a = c and b = d.
Here, a, b, c, and d are real numbers.
Here are some examples:
3 + 5i = (7 - 4) + 5i since 3 = 7 - 4
8 + 2i = 8 + (1 + 1)i since 2 = 1 + 1
Note:
8 + 7i = 7i + 8 since the real part of each complex
number is 8 and the imaginary part of
each is 7.
|