Fractions
A. Parts of a fraction:
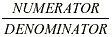
The numerator represents the number of parts of the unit being
used.
The denominator represents the total number of parts within
the one whole unit.
B. Types of fractions:
1. Proper fractions: fractions where the
numerator is less than the denominator.
Examples include:
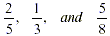
2. Improper fractions: fractions where the
numerator is greater than the denominator.
Examples include:
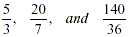
3. Mixed number fractions: numbers that
contain a whole number and a fraction.
Examples include:
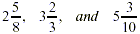
4. Fractions in lowest terms: fractions where
the numerator and denominator cannot be divided by a common
number.
Examples include:
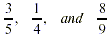
Examples of fractions that are not in lowest terms include:
a. 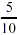 because 5 and 10 are both divisible by 5 to become
because 5 and 10 are both divisible by 5 to become 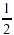
b. 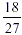 because 5 and 10 are both divisible by 5 to become
because 5 and 10 are both divisible by 5 to become 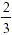
Operations with fractions:
When ADDING or SUBTRACTING FRACTIONS, all denominators have to
be the same number. If all denominators are not the same, you
must find the lowest common denominator. The lowest common
denominator is the smallest number that all the denominators will
divide into evenly. After you find the common denominator, you
must change each fraction into an equivalent fraction. An
equivalent fraction has the same value as the original fraction
but accommodates the new denominator. Once you find the common
denominator and change the fractions into equivalent fractions,
ADD or SUBTRACT the numerators, but do not add or subtract the
denominators. Keep the common denominator as part of the answer.
Reduce the answer to its lowest term if needed.
ADD:
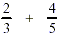 Find the lowest common denominator, lcd.
Find the lowest common denominator, lcd.
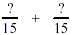 15 is the lcd. Make the equivalent fractions. 3 will divide into
15
15 is the lcd. Make the equivalent fractions. 3 will divide into
15
5 times. 5 times 2 = 10…. 5 will divide into 15
3 times. 3 times 4 = 12.
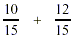 Add the numerators and keep the denominator. Reduce answer
Add the numerators and keep the denominator. Reduce answer
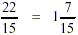 to its lowest term.
to its lowest term.
When multiplying and dividing fractions, it is not necessary
to find a common denominator. When multiplying fractions,
multiply numerators together then multiply denominators together.
Simplify the resulting fraction to its lowest term.
Ex: 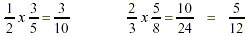
Note: Cancellation may be used if any
numerator will simplify with any denominator.
Ex: 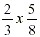 the numerator 2 will divide into itself 1 time and
into the denominator 8 times. the numerator 2 will divide into itself 1 time and
into the denominator 8 times.
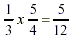
Ex: 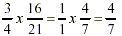
Divide: When dividing fractions, invert the
second fraction and multiply.
Ex: 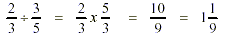
|