Adding and Subtracting Rational Expressions with Identical Denominators

We can multiply or divide any rational expressions, but we add or subtract only rational expressions with identical denominators. So when the denominators are not the same, we must find equivalent forms of the expressions that have identical denominators. In this section we will review the idea of the least common denominator and will learn to use it for addition and subtraction of rational expressions.

It is easy to add or subtract fractions with identical denominators. For example,

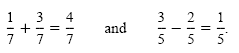
In general, we have the following definition.

Addition and Subtraction of Rational Numbers

If b ≠ 0, then

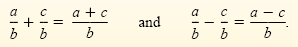
Rational expressions with identical denominators are added or subtracted in the same manner as fractions.

Example 1

Identical denominators

Perform the indicated operations.

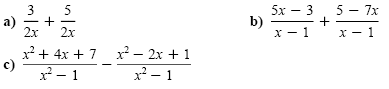
Solution

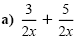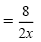		Add the numerators.
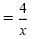		Reduce.

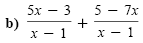		Add the numerators.
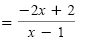		Combine like terms.
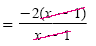		Factor.
	= -2	Reduce to its lowest terms.

c) The polynomials in the numerators are treated as if they were in parentheses:

Helpful hint

You can remind yourself of the difference between addition and multiplication of fractions with a simple example: If you and your spouse each own 1/7 of Microsoft, then together you own 2/7 of Microsoft. If you own 1/7 of Microsoft, and give 1/7 of your stock to your child, then your child owns 1/49 of Microsoft.