The Cartesian Coordinate System
The Cartesian coordinate system consists of two real number lines
placed at right angles to each other.
The horizontal number line is called the x-axis.
The vertical number line is called the y-axis.
The axes define a flat surface called the xy-plane.
Every point in the xy-plane has two numbers associated with it.
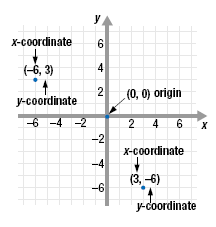
• The x-coordinate or abscissa tells how far the point lies to the left or
right of the y-axis.
• The y-coordinate or ordinate tells how far the point lies above or below
the x-axis.
The x-coordinate and the y-coordinate are often written inside parentheses,
like this: (x, y).
The first number, x, represents the x-coordinate and the second number,
y, represents the y-coordinate.
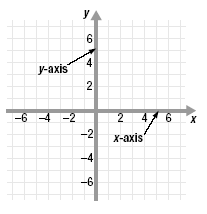
For example, the point that is 3 units to the right of the y-axis and 6 units
below the x-axis is labeled (3, -6).Because the order in which the pair of numbers is written is important,
(x, y) is called an ordered pair. Thus, the point (-6, 3) is not the same as
the point (3, -6).
The x-axis and the y-axis intersect at the point (0, 0). This point is called
the origin.
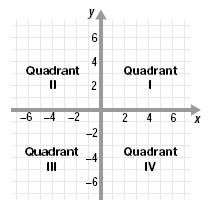
The x-axis and the y-axis divide the xy-plane into four regions called quadrants.
| Quadrant
I
II
III
IV |
Sign of x
positive
negative
negative
positive |
Sign of y
positive
positive
negative
negative |
A point on an axis does not lie in a quadrant.
Example 1Find the coordinates of each point
labeled on the graph.
Then, state the quadrant in which
each point lies.
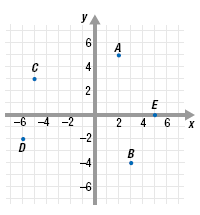
Solution
Point A has coordinates (2, 5), and lies in Quadrant I.
Point B has coordinates (3, -4), and lies in Quadrant IV.
Point C has coordinates (-5, 3), and lies in Quadrant II.
Point D has coordinates (-6, -2), and lies in Quadrant III.
Point E has coordinates (5, 0). It is not in a quadrant since it lies on the
x-axis.
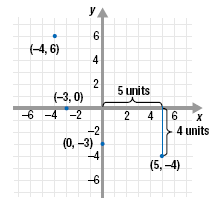
Example 2
Plot each point on a Cartesian coordinate system:
a. (5, -4)
b. (-4, 6)
c. (-3, 0)
d. (0, -3)
Solution
The plot the point (5, -4), start at the origin:
• move 5 units to the right;
• then move down 4 units;
• place a dot at this location.
Follow a similar procedure for the other points. Notice the difference
between the locations of points (-3, 0) and (0, -3).
|