Rotating Axes
You probably know already that equations of conics with axes parallel to one of the
coordinate axes can be written in the general form
| Ax2 + Cy2 + Dx + Ey + F = 0 |
Horizontal or vertical axes |
Here you will study the equations of conics whose axes are rotated so that they are not
parallel to the x-axis or the y-axis. The general equation for such conics contains an
xy-term.
| Ax2 + Bxy + Cy2 + Dx + Ey + F = 0 |
Equation in xy-plane
|
To eliminate this xy-term, you can use a procedure called rotation of axes. You want
to rotate the x- and y-axes until they are parallel to the axes of the conic. (The rotated
axes are denoted as the x'-axis and the y'-axis, as shown in the figure below.)
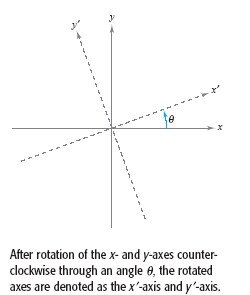
After the
rotation has been accomplished, the equation of the conic in the new x'y'-plane will
have the form
| A'(x')2 + B'x'y' + C'(y')2 + D'x' +
E'y' + F' = 0 |
Equation in x'y'-plane
|
Because this equation has no x'y'-term, you can obtain a standard form by completing
the square.
The following theorem identifies how much to rotate the axes to eliminate an
xy-term and also the equations for determining the new coefficients A', C', D',
E',
and F'.
THEOREM 1
Rotation of Axes
The general equation of the conic
Ax2 + Bxy + Cy2 + Dx + Ey + F = 0
where B ≠ 0, can be rewritten as
A'(x')2 + B'x'y' + C'(y')2 + D'x' + E'y' + F' = 0
by rotating the coordinate axes through an angle
θ, where
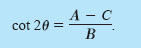
The coefficients of the new equation are obtained by making the substitutions
x = x' cos θ - y' sin θ
y = x' sin θ + y' cos θ.
Proof
To discover how the coordinates in the xy-system are related to the coordinates
in the x'y'-system, choose a point P = (x, y) in the original system and attempt to find
its coordinates (x', y') in the rotated system. In either system, the distance r between
the point P and the origin is the same, and thus the equations for x, y, x', and
y' are
those given in the figure below.
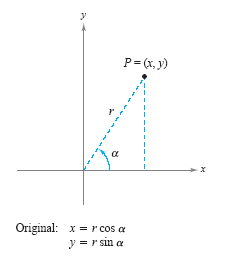 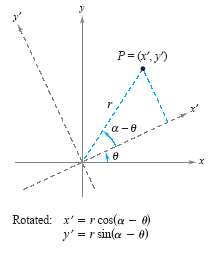
Using the formulas for the sine and cosine of the difference
of two angles, you obtain
| x' = r cos (α -
θ) |
= r (cos α cos θ
+ sin α sin θ) = r cos α cos θ + r
sin α sin θ = x cos θ + y sin
θ |
| y' = r sin (α -
θ) |
= r (sin α cos θ
- cos α sin θ) = r sin α cos θ - r
cos α sin θ = y cos θ - x sin
θ |
Solving this system for x and y yields
x = x' cos θ - y' sin θ and y = x' sin
θ + y' cos θ.
Finally, by substituting these values for x and y into the original equation and collecting
terms, you obtain the following.
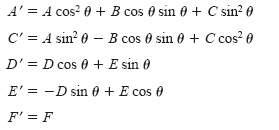
Now, in order to eliminate the x'y'-term, you must select
θ such that B' = 0, as
follows.
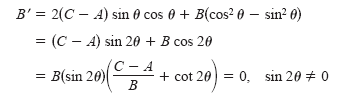
If B = 0, no rotation is necessary, because the xy-term is not present in the original
equation. If B ≠ 0, the only way to make B'
= 0 is to let
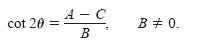
Thus, you have established the desired results.
|