Adding and Subtracting Fractions with Like Denominators
Example 1
Adding Fractions with Like Denominators
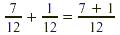 Write as a sum over a common
denominator. Write as a sum over a common
denominator.
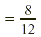 Add the numerators. Add the numerators.
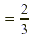 Simplify the fraction. Simplify the fraction.
Example 2
Subtracting Fractions with Like Denominators
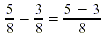 Write as a difference over a common
denominator. Write as a difference over a common
denominator.
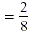 Subtract the numerators. Subtract the numerators.
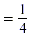 Simplify the fraction. Simplify the fraction.
Use the same rule when adding or subtracting three or more
fractions with like denominators.
Example 3
Real-Life Application
FOREST FIRES
A forest fire advances mile during the first hour, mile during
the second hour, and mile during the third hour. How far does the
forest fire advance in the first three hours?
Solution
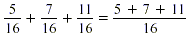 Add the numerators. Add the numerators.
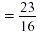 Write as a sum over a common denominator. Write as a sum over a common denominator.
The forest fire advances 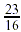 or or 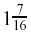 miles. miles.
|