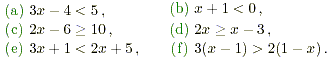|
Tuesday 21st of January |
InequalitiesRules for InequalitiesThe section following this one will deal with the solution of inequalities. As with the solution of equations, there are certain rules that may be used. In the case of inequalities these are Rule 1 An equal quantity may be added to, (or subtracted from) both sides of an inequality without changing the inequality. Rule 2 An equal positive quantity may multiply (or divide) both sides of an inequality without changing the inequality. Rule 3 If both sides of an inequality are multiplied (or divided) by a negative quantity then the inequality is reversed . N.B. It is very important to be careful with the last rule. Before looking at the solution of inequalities it is useful to see why the above rules hold. This is done in the following example. Example 1 Given the (true) inequality 4 > - 1, verify each of the rules (a) by adding 3 to both sides, (b) by subtracting 3 from both sides, (c) by multiplying both sides by 3, (d) by multiplying both sides by - 3. Solution (a) Adding 3 to both sides gives 7 > 2, which is also true. (b) Subtracting 3 from both sides gives 4 - 3 > - 1 - 3 or 1 > - 4, which is also true. (c) Multiplying both sides by 3 gives 12 > -3, which is also true. (d) Multiplying the inequality 4 > -1 by -3 gives. according to rule 3, 4 × (-3) < (-1) ×(-3), or -12 < 3, which is correct. Solving InequalitiesExample 2 Solve the following inequalities. (a) x - 3 > 5, (b) 2x - 1 > 7, (c) 3 - 2x > -5. Solution (a) x - 3 > 5, add 3 to both sides x - 3 + 3 > 5 + 3, x > 8 . (b) 2x - 1 > 7 , add 1 to both sides 2x > 8 , divide both sides by 2, x > 4. (c) 3 - 2x > -5, subtract 3 from both sides -2x > -8 , divide both sides by - 2 x < 4, rule 3 has reversed the inequality! Here are some exercises on solving inequalities. Exercise Solve each of the following inequalities using the rules given in section 2.
Solutions (a) 3x - 4 < 5 3x - 4 + 4 < 5 + 4 3x < 9 x < 3. (b) x + 1 < 0 x + 1 - 1 < 0 - 1 x < - 1 (c) 2x - 6 2x - 6 + 6 2x x (d) 2x 2x - x x (e) 3x + 1 < 2x + 5 3x + 1 - 1 < 2x + 5 - 1 3x < 2x + 4 3x - 2x < 2x + 4 - 2x x < 4 (d) In this case the brackets must first be removed using the standard rules. 3(x - 1) > 2(1 - x) 3x - 3 > 2 - 2x 3x - 3 + 3 > 2 - 2x + 3 3x > 5 + 2x 3x - 2x > 5 + 2x - 2x x > 5 Now try this short quiz. Quiz Which of the following is the solution to the inequality 15 - x > 7 + x ? (a) x > 4, (b) x > 11, (c) x Solution The solution is as follows. 15 - x > 7 + x 15 - x + x > 7 + x + x 15 > 7 + 2 x 15 - 7 > 7 + 2 x - 7 8 > 2 x 4 > x or equivalently x < 4 The first step in this solution was adding x to both sides so that (the positive) 2x appears on the right. This meant that the subsequent division was by the positive number 2. Division by positive numbers is always preferable as it generally leads to fewer mistakes.
|
|