Intercepts of a Line
Example
Given the equation 4x - 3y = 12:
a. Find the x-intercept.
b. Find the y-intercept.
c. Use the intercepts to graph the line.
| a. |
Solution
The x-intercept has the form (a, 0).
To find the x-intercept, substitute 0
for y.
Then solve for x.
Simplify.
Divide both sides by 4.
The x-intercept is (3, 0). |
4x - 3y
4x - 3(0)
4x
x |
= 12
= 12
= 12
= 3 |
| b. |
The y-intercept has the form (0, b).
To find the y-intercept, substitute 0
for x.
Then solve for y.
Simplify.
Divide both sides by -3.
The y-intercept is (0, -4). |
4x - 3y
4(0) - 3y
-3y
y |
= 12
= 12
= 12
= -4
|
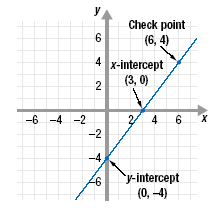
| c. |
To graph the line 4x - 3y = 12, plot the x-intercept and the
y-intercept.
Then, draw a line through the intercepts.
As a check, it is a good idea to find a third point on the line.
For example, choose 6 for x in the equation 4x - 3y = 12.
Solve for y. The result y = 4.
Since (6, 4) is a solution of the equation 4x - 3y = 12, the line should
pass through the point (6, 4). |
|
x |
y |
|
|
3 |
0 |
x-intercept |
|
0 |
-4 |
y-intercept |
|
6 |
4 |
check point |
|
 |
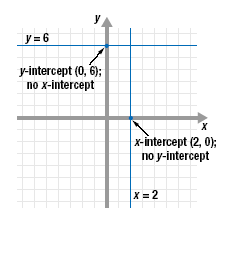
Some lines do not have both an x-intercept and a y-intercept.
• A horizontal line, other than the x-axis, has a y-intercept, but
no x-intercept.
For example, the horizontal line y = 6 has y-intercept (0, 6), but no
x-intercept.
• A vertical line, other than the y-axis, has an x-intercept, but
no y-intercept.
For example, the vertical line x = 2 has x-intercept (2, 0), but no
y-intercept.
|