Solving Exponential Equations
Example 1
Solve:
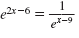
Solution
Each side of the equation contains an expression with base e. However, in
the expression on the right, the base e is in the denominator.
Therefore, we use the definition of a negative exponent to write the
expression on the right with in the numerator.
| Original equation.
|
e2x - 6 |
 |
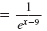| Rewrite the right side.
Remove the parentheses.
Use the Exponential Equality Property.
Add x to both sides.
Add 6 to both sides.
Divide both sides by 3. |
e2x - 6
e2x - 6
2x - 6
3x - 6
3x
x |
= e -(x - 9)
= e - x + 9
= -x + 9
= 9
= 15
= 5 |
So, the solution of
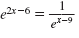is x = 5.
Note:
Recall the definition of a negative
exponent:
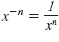
Example 2
The point (2, 25) lies on the graph of the exponential function y
= bx.
Find the base, b, of this exponential function.
Solution
| Since (2, 25) lies on the graph, we know that x
= 2 when y = 25 in the exponential function. |
y |
= bx |
| Replace y with 25 and x with 2.
Write 25 as 52.
Since the exponents are the same, the bases
are equal.
So, the base, b, of the exponential function is 5.
We can now write the exponential function:
As a check, find f(2). |
25
52
5
f(x)
f(2) |
= b2
= b2
= b
= 5x
= 52
= 25 |
This results in the original ordered pair, (2, 25), as expected.
Note:
Note that if 52 = b2 then b could
also be -5.
However, we are working with an
exponential function.
That means the base,
b, must be such that b > 0 and b
≠ 1.
Thus, b must be positive 5.
|
