Exponential Growth
An exponential function of the form f(x) = bx has base b, where b is a real
number, b > 0, and b ≠ 1.
An exponential growth function is an exponential function where b > 1. The graph of an exponential growth function
increases when moving from
left to right.
Let’s look at the graphs of two exponential growth functions:
f(x) = 2x and f(x) = 3x
Note:
Examples of exponential growth functions
are population growth and compound
interest earned on money invested.
From the graphs, notice the following:
• Each graph increases when moving from left to right (because b
> 1).
• Both graphs intersect the y-axis at (0, 1).
• When x < 0, the graph of the function with the smaller base, y
= 2x, lies above the graph of the function with the larger base, y
= 3x.
• When x > 0, the graph of the function with the smaller base, y = 2x, lies
below the graph of the function with the larger base, y = 3x.
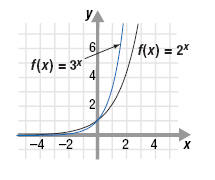
• Each graph passes the vertical and horizontal line tests. Therefore,
each graph represents a one-to-one function.
• The domain of each function is all real numbers.
• The range of each function is all positive real numbers.
|