FOIL Method

When it comes to expanding a bracket like ( a + c )( x + y ) there is a simple way to remember all of the terms. This is the word FOIL, and stands for

take products of the

First Outside Inside Last

This is illustrated in the following.

Example

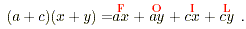
These terms are the products of the pairs highlighted below.

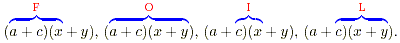
There are two other brackets that are worth remembering. These are

( x + y) ², which is a complete square, and

( x + y)( x - y) , which is a difference of two squares.

These are included in the following exercises.

Exercise

Remove the brackets from each of the following expressions using FOIL.

(a) ( x + y) ²

(b) ( x + y)( x - y)

(c) ( x + 4)( x + 5)

(d) ( y + 1)( y + 3)

(e) (2 y + 1)( y - 3)

(f) 2( x - 3) ² - 3( x + 1) ²

Solution

(a)

This is an IMPORTANT result and should be committed to memory. Here x is the first member of the the bracket and y is the second. The rule for the square of ( x + y ), i.e. ( x + y ) ² is

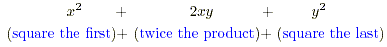
(b) Using FOIL again:

The form of the solution is the reason for the name difference of two squares. This is another important result and is worth committing to memory.

(c) Using FOIL :

(d) Using FOIL :

(e) Using FOIL :

(f) This one is best done in parts. First we have

( x - 3) ² = x ² - 6 x + 9

and

( x + 1) ² = x ² + 2 x + 1

Thus

Quiz

To which of the following expressions does 9 - ( x -3) ² simplify?

(a) - x ²

(b) 6 x - x ²

(c) 18 - x ²

(d) 6 x + x ²

Solution

First note that ( x - 3) ² = x ² - 6 x + 9, so