|
Conics in Standard Form
The standard form of conics is of the form ax2 + by2 +
2gx + 2fy + c = 0. While this form
is easier to use with algebra, it does not tell us much about the shape of the conic, or any
of its properties.
Special properties of the form ax2 + by2 + 2gx + 2fy +
c = 0
· For a circle a = b
· For an ellipse a and b have the same sign and a
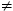 b b
· For a parabola, either a = 0 or b = 0
· For a hyperbola a and b have opposite signs
Example 1
Identify the conic and write in standard form the conic which is defined as
4x2 + 9y2 - 16x + 18 - 11 = 0
Solution
Using the above, we see this is an ellipse. To find out the properties of the ellipse, we
need to complete the square for both sides:
| 4x2 + 9y2 - 16x
+ 18y - 11 |
= 0 |
| 4x2 - 16x + 9y2
+ 18y |
= 11 |
| 4(x2 - 4x) + 9(y2 +
2y) |
= 11 |
| 4(x2 - 4x+ 4 - 4) + 9(y2
+ 2y + 1 - 1) |
= 11 |
| 4(x - 2)2 - 16 + 9(y + 1)2
- 9 |
= 11 |
| 4(x - 2)2 + 9(y + 1)2 |
= 36 |
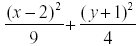 |
= 1 |
Example 2
Find the equation of the conic for y2 + 8x + 2y - 15 = 0
Solution
a=0, so this is a parbola.
| y2 + 8x + 2y - 15 |
= 0 |
| y2 + 8x + 2y |
= 15 |
| (y2 + 2y + 1 - 1) + 8x |
= 15 |
| (y + 1)2 + 8x |
= 15 |
| 8x - 16 |
= 16 |
| 8(x - 2) |
= -(y + 1)2 |
| x - 2 |
= -(y + 1)2 |
| x - 2 |
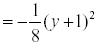 |
|