Graphing Logarithmic Functions
Example
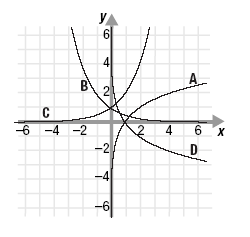
Graphs A, B, C, and D represent functions of the form y = bx and y
= logbx, where b is the base of each function. Here, b > 0 and b
≠ 1.
a. Which graph represents an exponential function where b > 1?
b. Which graph represents an exponential function where 0 < b < 1?
c. Which graph represents a logarithmic function where b > 1?
d. Which graph represents a logarithmic function where 0 < b < 1?
Solution
a. Graph C. Because b > 0, the y-values of an exponential function will
all be positive. Also, because b > 1, as the x-values increase, the
y-values will increase. (The function for graph C is y = 2x.)
b. Graph B. Because b > 0, the y-values of an exponential function will
all be positive. Because 0 < b < 1, as the x-values increase, the
y-values will decrease. (The function for graph B is
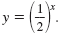 ) )
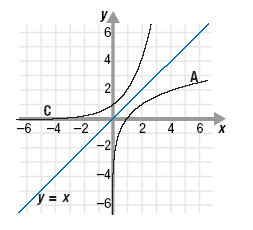
c. Graph A. The inverse of a logarithmic function where b > 1 is an
exponential function where b > 1. If the graph of an exponential
function where b > 1 (such as graph C) is reflected across the line
y = x, we obtain a graph like graph A. (The function for graph A is
y = log2x.)
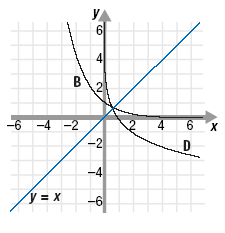
d. Graph D. The inverse of a logarithmic function where 0 < b < 1 is an
exponential function where 0 < b < 1. If the graph of an exponential
function where 0 < b < 1 (such as graph B) is reflected across the line
y = x, we obtain a graph like graph D. (The function for graph D is
y = log 1/2 x.)
|