Simplifying Cube Roots That Contain Variables
Next we will simplify a cube-root radical whose radicand contains a
variable.
We will use a procedure similar to the one we used to simplify square-root
radicals. However, when we simplify a cube-root radical, we divide the
exponent of the variable by 3 (instead of 2).
Here are some examples.
If x is any real number, then:
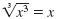 since
x · x · x = x3 since
x · x · x = x3 |
|
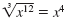 since
x4 · x4
· x4 = x12 since
x4 · x4
· x4 = x12 |
Notice that
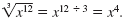 |
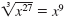 since
x9 · x9
· x9 = x27 since
x9 · x9
· x9 = x27 |
Notice that
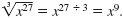 |
In each example, the exponent of the variable in the simplified expression
is one-third the exponent of the variable in the radicand.
Be careful:
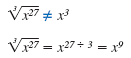
If the power of x in the radicand is not a multiple of 3, we rewrite the
radicand as a product where one of the factors has a power that is a
multiple of 3 and the other factor is x1 or x2.
For example, let’s simplify
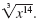 |
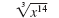 |
| Write x14 as x12
· x2. |
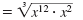 |
| Notice that 12 is a multiple of 3.
|
|
| Write as the product of two radicals.
|
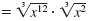 |
| Simplify. |
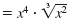 |
So,
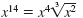
Example
Simplify:
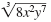
| Solution |
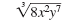 |
| Factor the radicand, using perfect
cube factors when possible.
|
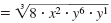 |
| Write as a product of four radicals.
|
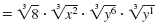 |
| Simplify the cube root of each perfect
cube. |
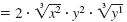 |
| Combine the remaining radicals. |
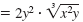 |
So,
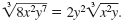
|