Solving Systems of Equations Using Elimination
Objective: Solve systems of linear equations
using elimination
Example 1)
| 3 x + 2 y = 2 -3 x + 2 y = 6
|
Add the equations |
| 4 y = 8 |
Simplify |
| y = 8/4 = 2 |
|
| |
Substitute using y = 2 |
| 3 x + 2(2) = 2 |
|
| 3 x + 4 = 2 |
Simplify |
| 3 x = -2 |
|
| x = -2/3 |
Solution (-2/3, 2) |
Example 2)
| - x - y = 8 -2 x - y = -1
|
Subtract the equations |
| x = 9 |
Substitute using x = 9 |
| -9 - y = 8 |
|
| - y = 17 |
|
| y = -17 |
Solution (9, -17) |
Example 3)
| 2 x = -3 y + 1 x + 2 y = -1
|
Rewrite in standard form |
| 2 x + 3 y = 1 x + 2 y = -1
|
Multiply the 2nd equation by -2 then add |
| 2 x + 3 y = 1 -2 x - 4 y = 2
|
Simplify |
| -y = 3 y = -3
|
Substitute using y = -3 |
| x + 2(-3) = -1 x + -6 = -1
x = 5
|
Solution (5, -3) |
Example 4)
| 3 x + 2 y = 1 2 x - 5 y = -2
|
Let’s eliminate the x |
| -2(3 x + 2 y ) = -2 (1) 3(2 x - 5 y )
= 3(-2)
|
Multiply the first equation
by -2 Multiply the 2nd equation by 3
|
| -6 x - 4 y = -2 6 x - 15 y = -6
|
Now add. |
| -19 y = -8 y 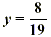
|
Now substitute |
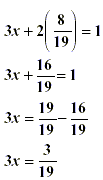 |
Simplify. |
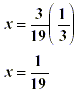 |
Solution: 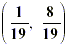 |
|