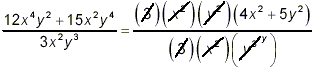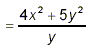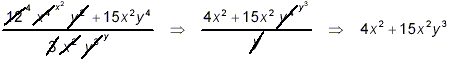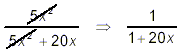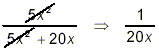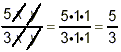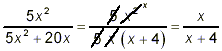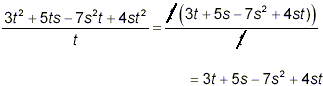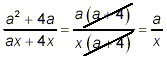|
Tuesday 21st of January |
Simplifying FractionsExamples with solutions
Example 1: Simplify solution: Since the numerator is the sum of two terms, we must begin by factoring it as much as possible:
Thus
as the final answer. The initial factoring step is absolutely essential. If instead you decided to begin by cancelling between the denominator and the first term of the numerator, along the lines of
you would end up with a completely wrong result. This kind of thing is not wrong so much because we say so, or because you didn’t use “our” method, the method “we” told you to use. Rather, it is wrong because the result does not have the same mathematical meaning, nor will it give the same mathematical results as the original expression, and so it’s about the same sort of thing as deciding the change the meaning of words when you speak (but pretending you haven’t!). If you substitute specific pair of values for x and y into this proposed simplified expression, you will get different value from it than you would get when you substitute the same values of x and y into the original expression. Simplification is intended to give a mathematical expression which is easier to write down and work with than the original expression, but which gives exactly the same results as the original expression in all circumstances. If our apparent simplified expression does not do this, then we have made a mistake.
Example 2: Simplify solution: It is so tempting just to cancel the ‘5x 2’ terms and be done:
or even
By now you’re screaming back, “No! No! Both of these results are wrong! Wrong! Wrong!” In both cases, the that is being cancelled is not a factor in the denominator (it is a “term” in the denominator) and hence cannot be validly cancelled. In the second version above, another error is made as well. When factors are cancelled, they always leave a result of “1” behind. If it is a multiplication by 1, we need not write down the 1, as in
But, if it is an “added” 1, you cannot drop it: (1)(20x) = 20x but (1) + (20x) This latter is as incorrect as writing
This is supposed to look like a fraction with nothing written in the numerator or in the denominator (that is, the ultimate in cancellation – perhaps we should consider this to be annihilation!). Of course, you can easily see this is nonsense. Anyway, back to the original example. Before any cancelling can be contemplated, both the numerator and denominator must be factored completely. The numerator is already in factored form. However, for the denominator we have 5x 2 + 20x = 5[x 2 + 4x] = 5x(x + 4) Thus
as the final correct answer.
Example 3: Simplify solution: The denominator is obviously fully factored. For the numerator, only slight factoring is possible: 3t 2 + 5ts - 7s 2 t = t (3t + 5s - 7s 2 + 4st ) Therefore
as the final simplified form.
Example 4: Simplify solution: First, factoring a 2 + 4a = a (a + 4) and ax + 4x = x (a + 4) Thus
as the final simplified result. |
|