Roots of Complex Numbers
Recall that a consequence of the Fundamental Theorem of Algebra is that a polynomial
equation of degree n has n solutions in the complex number system. Each
solution is an nth root of the equation. The nth root of a complex number is defined
as follows.
Definition of nth Root of a Complex Number
The complex number u = a + bi is an nth root of the complex number z if
z = un = (a + bi)n.
STUDY TIP
The nth roots of a
complex number are useful for solving
some polynomial equations. For
instance, you can use DeMoivre’s
Theorem to solve the polynomial
equation x4 + 16 = 0
by writing -16 as 16(cos π + i sin π).
To find a formula for an nth root of a complex number, let u be an nth root of z,
where u = s(cos β + i sin β)
and z = r(cos θ + i sin θ).
By DeMoivre’s Theorem and the fact that un = z you have
sn(cos nβ + i sin nβ) = r (cos
θ + i sin θ).
Taking the absolute values of both sides of this equation, it follows that sn
= r.
Substituting back into the previous equation and dividing by r, you get
cos nβ + i sin nβ = cos
θ + i sin θ
Thus, it follows that
cos nβ = cos
θ and sin nβ = sin θ.
Because both sine and cosine have a period of 2π,
these last two equations have
solutions if and only if the angles differ by a multiple of 2π.
Consequently, there must
exist an integer k such that
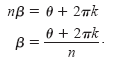
By substituting this value for into the polar form of u, you get the following result.
NOTE
When k exceeds n - 1 the
roots begin to repeat. For instance, if k = n
the angle
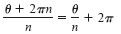 is coterminal with θ/n which is also
obtained when k = 0.
is coterminal with θ/n which is also
obtained when k = 0.
Theorem
nth Roots of a Complex Number
For a positive integer n, the complex number z = r(cos
θ + i sin θ) has exactly n
distinct nth roots given by
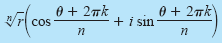
where k = 0, 1, 2, ..., n - 1.
This formula for the nth roots of a complex number z has a nice geometrical
interpretation, as shown in the figure below.
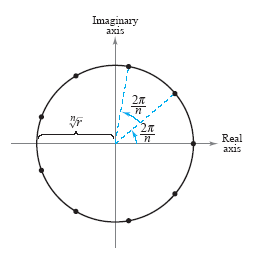
Note that because the nth roots of z all have
the same magnitude
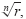 they all lie on a circle of radius they all lie on a circle of radius
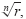 with center at the origin.
Furthermore, because successive nth roots have arguments that differ by 2π/n,
the n
roots are equally spaced along the circle. with center at the origin.
Furthermore, because successive nth roots have arguments that differ by 2π/n,
the n
roots are equally spaced along the circle.
Example 1
Finding the nth Roots of a Complex Number
Find the three cube roots of z = -2 + 2i.
Solution
Because z lies in Quadrant II, the polar form for z is
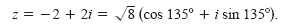
By the formula for nth roots, the cube roots have the form
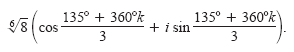
Finally, for k = 0, 1, and 2, you obtain the roots
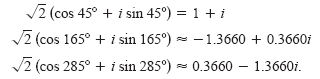
|