Multiplication Property of Equality

Examples

Example 1:

Solve

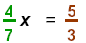	Multiply recip:
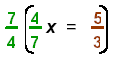	Distributive Property
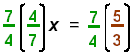	Associative Property
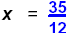	Recall

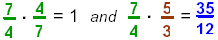Example 2:

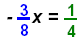	Multiply recip:
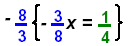	Distributive Property
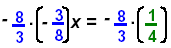	Associative Property
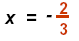	Note
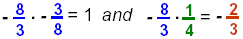Check:	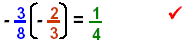Replace x with 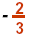to check.

Solve Equation with a Balance Beam

Pattern: ax + b = cx + d

Both sides siimplliiffiied (a ,b, c, d are integers.)

Look at the coefficients of x and determine which is the larger integer (furthest to the right on the number line). If c > a then we will keep the variiablle x on tthatt siide of the equation and keep the constant on the other side. To do this we first add opposites on the balance beam below the equation. Look at the pattern, and then follow the same steps through several examples

Solve simplified equations vertically - using the balance beam.

Pattern: c > a

1) Add opps:

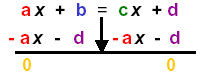
Complete the step: (b - d) = (c - a)x → Let A = (c - a) and B = (b - d)

Then: B = A x → A > 1 is coefficient of x

2) Multiply recip:

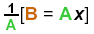
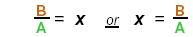→ Since

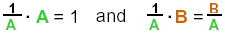
Example 3:

Solve

1) Add opps:		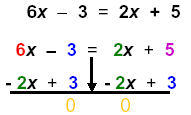Note that 6 > 2 (Add same to both sides)
Complete the step:	(6 - 2)x = (5 + 3)	Now (6 - 2) = 4 and (5 + 3) = 8 4 is the coefficient of x
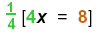
2) Multiply recip: Then	x = 2	Since
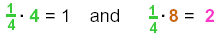3) Check:		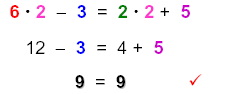Note that 6 · 2 = 12   x = 2 is correct.