Solving Quadratic Equations by Completing the Square
There are some equations where the solutions are rational numbers, and the
equation
can be solved by factoring.
In the next example the solutions are irrational
numbers, and factoring will not work.
Example 1
A quadratic equation with irrational solutions
Solve x2 - 3x - 6 = 0 by completing the square.
Solution
Because a = 1, we first get the x2 and x terms on the left-hand side:
| x2 - 3x - 6 |
= 0 |
|
| x2 - 3x |
= 6 |
Add 6 to each side. |
 |
 |
 |
 |
 |
 |
 |
 |
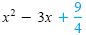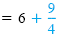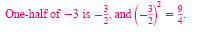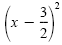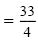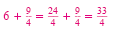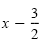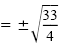Even-root property |
| x |
 |
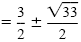Add
 to each side.
|
| x |
 |
|
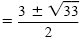The solution set is
 .
|
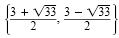