Graphing Linear Functions
We can graph a linear function by calculating two ordered pairs, plotting
the corresponding points on a Cartesian coordinate system, and then
drawing a line through the points. We typically calculate and plot a third
point as a check.
To find ordered pairs, we select values for x and then calculate the
corresponding values for y. Thus, the output value y depends on our choice
of the input value x. For this reason, the variable y is frequently called the
dependent variable and the variable x is called the independent
variable.
Example 1
Make a table of at least three ordered pairs that satisfy the function
f(x) = 3x - 1. Then, use your table to graph the function.
Solution
To make a table, select 3 values for x. We’ll let x = -2, 0, and 2.
Substitute the values of x into the function and simplify.
|
x |
f(x) = 3x - 1 |
(x, y) |
|
-2 0
2 |
f(-2) = 3(-2) - 1 = -6 - 1 = -7 f(0) = 3(0) - 1 = 0 - 1 = -1
f(2) = 3(2) - 1 = 6 - 1 = 5 |
(-2, -7) (0, -1)
(2, 5) |
Now, plot the points (-2, -7), (0, -1), and (2, 5) and then draw a line
through them.
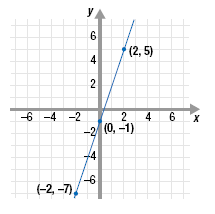
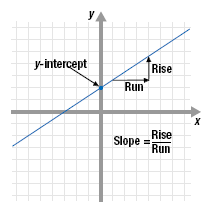
Two important characteristics of the graph of a linear function are its y-intercept and its
slope.
• The y-intercept is the point where the line crosses the y-axis.
• The slope measures the steepness or tilt of the line. Slope is defined as
the ratio of the rise to the run of the line. When moving from one point
to another on the line, the rise is the vertical change and the run is the
horizontal change.
The linear function, f(x) = Ax + B, is another way of writing the familiar
slope-intercept form for the equation of a line, y = mx + b. In f(x) = Ax + B the slope of the line is given by A and the y-intercept is given by B.
f(x) = Ax + B is equivalent to y = mx + b
This means that the graphs of all linear functions are straight lines. That is
why such functions are called linear.
Example 2
Graph the function:
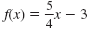
Solution
| This has the form of a linear function. |
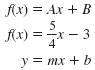 |
Thus, the slope is
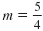 and the y-intercept is b
= -3. and the y-intercept is b
= -3.
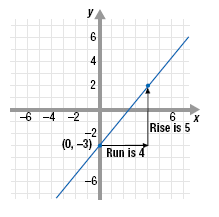
To graph the line, first plot the y-intercept; that is, plot the point (0, -3).
From this point rise in the y-direction 5 units (the numerator of the slope)
and run in the x-direction 4 units (the denominator of the slope). The new
location (4, 2) is a second point on the line.
Finally, connect the plotted points.
|