Solving Quadratic Equations by Graphing
Objective Understand why the solutions of a
quadratic equation occur where the graph of the corresponding
function intersects the x-axis.
Let's see some examples, where the goal is to find or
approximate the solutions to a quadratic equation ax 2
+ bx + c = 0 by looking to see where the graph of the
corresponding quadratic equation intersects the x-axis.
Example 1
Solve x 2 - x - 2 = 0 by graphing.
Solution
Step 1 Make a table of values, and then graph
the function y = x 2 - x - 2.
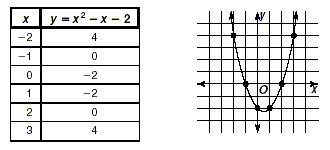
Step 2 Find where the parabola intersects the
x -axis. In this case, this occurs when x = -1 and x = 2. Thus, -
1 and 2 are the solutions to the equation x 2 - x - 2
= 0 .
Step 3 Check the answer by factoring.
0 = x 2 - x - 2
0 = ( x + 1)( x - 2)
Set each factor equal to zero.
| x + 1 = 0 |
x - 2 = 0 |
| x = -1 |
x + 2 |
So, the solutions check.
Example 2
Solve x 2 - 2x - 2 = 0 by graphing.
Solution
Step 1 Make a table of values, and then graph
the function y = x 2 - 2x - 2.
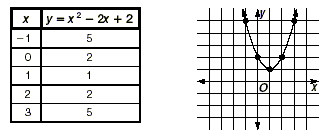
Step 2 Notice that the parabola does not
intersect the x-axis. This parabola opens upward and we can
compute that the vertex is at (1, 1). This vertex lies above the
x-axis, so the parabola never intersects the x-axis. We can
conclude that there are no solutions to the equation x 2
- 2x - 2 = 0.
Example 3
Solve 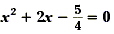 by graphing. by graphing.
Solution
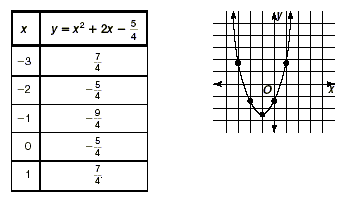
Step 1 Make a table of values, and then graph
the function 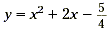 . .
Step 2 Try to factor and solve for the roots.
In this case, 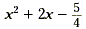 does not have integral
factors. does not have integral
factors.
Step 3 Use the graph to approximate the
solutions. We can see from the graph that the parabola intersects
the x -axis twice: once between -3 and -2, and once roughly
halfway between 0 and 1. We can therefore estimate solutions to
the equation 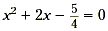 to be to be 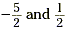 . (In this case, these
two estimates are actually exact solutions.) . (In this case, these
two estimates are actually exact solutions.)
In general, graphs provide a good way of approximating
solutions to quadratic equations when the corresponding quadratic
expressions cannot be factored with integral factors. In order to
get exact solutions, we need to use the Quadratic Formula, which
will be discussed in other lessons.
|