|
Friday 26th of April |
Solving EquationsSolving equations is a recurring theme in much of mathematics. We will study some of the principles used to solve equations and then use equations to solve applied problems. Solving equations is essential for problem solving in algebra. In this section, we study two of the most important principles used for this task. Equations and SolutionsWe have already seen that an equation is a number sentence stating that the expressions on either side of the equals sign represent the same number. Some equations, like 3 + 2 = 5 or 2x + 6 = 2(x + 3) are always true and some, like 3 + 2 = 6 or x + 2 = x + 3 are never true. In this text, we will concentrate on equations like 3x + 6 = 17 or 7x = 141 that are sometimes true, depending on the replacement value for the variable. Solution of an Equation: Any replacement for the variable that makes an equation true is called a solution of the equation. To solve an equation means to find all of its solutions. To determine whether a number is a solution, we substitute that number for the variable throughout the equation. If the values on both sides of the equals sign are the same, then the number that was substituted is a solution. Example 1 Determine whether 7 is a solution of x + 6 = 13 Solution We have
Since the left-hand and the right-hand sides are the same, 7 is a solution. Example 2 Determine whether 19 is a solution of 7x = 141. Solution We have
Since the left-hand and the right-hand sides differ, 19 is not a solution. The Addition PrincipleConsider the equation x = 7. We can easily see that the solution of this equation is 7. Replacing x with 7, we get 7 = 7, which is true. Now consider the equation x + 6 = 13. In Example 1, we found that the solution of x + 6 = 13 is also 7. Although the solution of x = 7 may seem more obvious, the equations x + 6 = 13 and x = 7 are equivalent. Equivalent Equations: Equations with the same solutions are called equivalent equations. There are principles that enable us to begin with one equation and end up with an equivalent equation, like x = 7, for which the solution is obvious. One such principle concerns addition. The equation a = b says that a and b stand for the same number. Suppose this is true, and some number c is added to a. We get the same result if we add c to b, because a and b are the same number. The Addition Principle: For any real numbers a, b, and c, a = b is equivalent to a + c = b + c. To visualize the addition principle, consider a balance similar to one a jeweler might use. (See the figure.) When the two sides of the balance hold quantities of equal weight, the balance is level. If weight is added or removed, equally, on both sides, the balance will remain level.
When using the addition principle, we often say that we “add the same number to both sides of an equation”. We can also “subtract the same number from both sides”, since subtraction can be regarded as the addition of an opposite. Example 3 Solve: x + 5 = -7. Solution We can add any number we like to both sides. Since is the opposite, or additive inverse, of 5, we add to each side: x + 5 = -7 x + 5 - 5 = -7 - 5 Using the addition principle: adding -5 to both sides or subtracting 5 from both sides. x + 0 = -12 Simplifying: x + 5 - 5 = x + 5 + (-5) = x + 0. x = -12 Using the identity property of 0. It is obvious that the solution of x = -12 is the number -12. To check the answer in the original equation, we substitute. Check:
The solution of the original equation is -12. In Example 3, note that because we added the opposite, or additive inverse, of 5, the left side of the equation simplified to x plus the additive identity, 0, or simply x. These steps effectively replaced the 5 on the left with a 0. When solving x + a = b for x, we simply add -a to (or subtract a from) both sides. Example 4 Solve: -6.5 = y - 8.4 The variable is on the right side this time. We can isolate y by adding 8.4 to each side: -6.5 = y - 8.4 This can be regarded as -6.5 = y + (- 8.4) -6.5 + 8.4 = y - 8.4 + 8.4 Using the addition principle: Adding 8.4 to both sides “eliminates” -8.4 on the right side. 1.9 = y Sice y - 8.4 + 8.4 = y + (-8.4) + 8.4 = y + 0 = y Check:
The solution is 1.9. Note that the equations a = b and b = a have the same meaning. Thus, -6.5 = y - 8.4 could have been rewritten as y-8.4 = -6.5. Example 5 Solve: Solution We have
The check is left to the student. The solution is The Multiplication PrincipleA second principle for solving equations concerns multiplying. Suppose a and b are equal. If a and b are multiplied by some number c , then ac and bc will also be equal. The Multiplication Principle: For any real
numbers a , b , and c , with c |
|



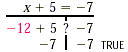
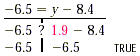
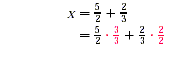 Multiplying by 1 to obtain a common denominator
Multiplying by 1 to obtain a common denominator