Negative Exponents
We started out by defining powers to be repeated
multiplications:
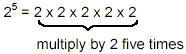
From this definition of the power or exponential notation,
several laws or properties could be inferred for powers of
products and quotients of numbers. These were described in the
preceding document in these notes.
One of those laws dealt with the quotient of two powers with
the same base. For example
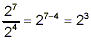
Of course, if the bigger power is in the denominator, the
result has the net power in the denominator:
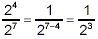
So far, both of these make sense when we consider powers to be
repeated multiplications, since only positive exponents occur in
both cases. However, if we simply subtracted the denominator
exponent from the numerator exponent in the second example, we
would have got
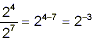 (*) (*)
At first, this result, with the negative exponent, appears a
bit nonsensical. We know how to multiply 2 by itself +3 times,
but it’s hard to imagine what it might mean to multiply 2 by
itself ‘-3’ times. The most useful way to get around
this apparent nonsense is adopt the rule that whenever we write 2
-3, we really mean 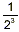 , that is: , that is:
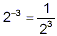
With this convention, results such as the one labelled (*)
make perfect sense.
So, if c is a nonzero number and n is a positive number (so
that –n is a negative number), we define
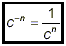
Remarks:
(i) This definition is consistent with all of the laws of
exponents given earlier, so the laws may be used with positive
and negative exponents.
(ii) When powers occur as a factor in the numerator or the
denominator of a fraction, the factors can be switched from top
to bottom or vice versa by changing the sign of the exponent.
Thus

(iii) Now we see, for example, that
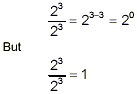
since the numerator and denominator are identical. By
comparing these last two expressions, we see that we can make
sense of 2 0 by defining it to be equal to 1, ie.
2 0 = 1
In general, if c is a nonzero number, we will define
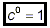
With this, we now have a reasonable way to interpret powers in
which the exponent is any whole number, positive or negative, or
zero. This will make the laws of exponents very helpful in
simplifying complicated expressions involving powers.
example:
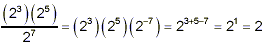
or

example:
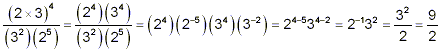
|