Solving Quadratic Equations
Factoring
Some Common Factoring Patterns
x 2 - a 2 = (x - a)
· (x + a) “Difference of two squaresâ€
x 2 + 2 · a
· x + a 2 = (x + a) 2 “Perfect square Iâ€
x 2 - 2 · a
· x + a 2 = (x - a) 2 “Perfect square IIâ€
Solving a Quadratic Equation
The objective of solving a quadratic equation:
a ·
x 2
+ b
·
x +
c =
0,
is to find the values of x
that make the quadratic formula equal to
zero. Graphically, these x-values
are the x-coordinates
of the points where the graph of
y =
a ·
x 2
+ b
·
x +
c
crosses the x-axis
(see Figure 2).
When you are trying to solve the quadratic equation
a · x
2 +
b ·
x +
c =
0, then what you are trying to do is to find the
x-coordinates
of any points where the graph of y
= a
·
x 2
+ b
·
x +
c crosses the
x-axis.
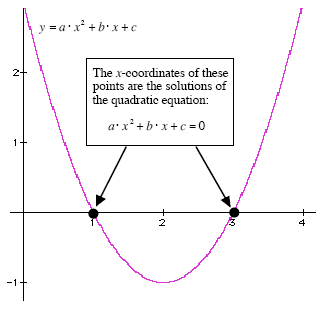
Figure 2: The solutions of a quadratic equation are the
x-coordinates
of the points where the graph of the quadratic cuts through the
x-axis.
|