Multiplying Special Polynomials
Multiplying Polynomials
Examples
Use the methods for multiplying binomials to multiply and simplify
the following.
1.Multiply and Simplify:
(3x + 5)(3x - 5) - (2x + 3)(2x - 3) Note that these are conjugates. Watch signs.
9
x2 - 25 - (4x2 - 9) Remove parentheses carefully:
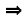 9x2
- 25 - 4x2 + 9 9x2
- 25 - 4x2 + 9
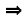 5x2
- 16 5x2
- 16
2. (3x + 5)2 - (2x + 3)2 Square the binomials and simplify.
Watch signs.
9x2 + 30x + 25 - (4x2 + 12x + 9) Remove parentheses carefully:
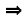 9x2 + 30x + 25
- 4x2 - 12x - 9 9x2 + 30x + 25
- 4x2 - 12x - 9
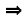 5x2 + 18x + 16 5x2 + 18x + 16
3. (2x + 3)3 Use the pattern in the example above then multiply a binomial times
polynomial
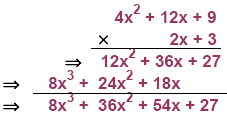
 (2x + 3)3 = 8x3 + 36x2
+ 54x + 27 (2x + 3)3 = 8x3 + 36x2
+ 54x + 27
Applications
1. Number Problem: Use the difference of squares to multiply 93 × 87 .
93 = 90 + 3 and 87 = 90 – 3
93 × 87 = (90 + 3)( 90 – 3) = 902 – 32
902 – 32 = 8100 - 9 = 8091
Check:
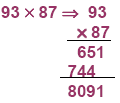
2. Number Problem: Write an expression for the sum of the squares of three
consecutive odd (or even) numbers. Then simplify the expression.
Let x be the first number, then x + 2 and x + 4 are the next two.
If x is odd
all are odd and if x is even all are even:
N = x2 + (x + 2)2 + (x + 4)2
N = x2 + (x2 + 4x + 4) + (x2 + 8x + 16)
N = 3x2 + 12x + 20
Check:
Odd: x = 3
32 + 52 + 72 = 9 + 25 + 49 = 83 or 3(3)2
+ 12(3) + 20 = 83

Even: x = 2
22 + 42 + 62 = 4 + 16 + 36 = 56 or 3(2)2 + 12(2) + 20 = 56

|