Adding and Subtracting Fractions

It is not difficult to visualize what it means to add two fractions, as in

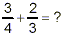
As explained before, each of the two fractions represents dividing a whole into a certain number of equal-sized pieces, and including a certain number of those pieces. So, we can represent the two fractions above pictorially as

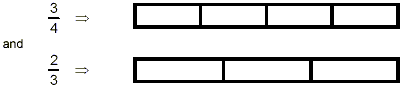
Thus, 3 / 4 represents 3 pieces, each of which is 1 / 4 of the whole, and 2 / 3 represents 2 pieces, each 1 / 3 of the whole. Then, to form the sum

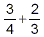
we need to come up with a fraction representing how much of a whole we get when we combine all five shaded pieces in the diagrams above. The difficulty is that we can’t just count up the number of shaded pieces to be 5 and the total number of pieces to be 7, and so declare the answer to be 5 / 7 (from 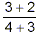), since the pieces are not all the same size to begin with. In fact, you can see that this answer would clearly be wrong, because it represents less than a complete whole, and yet it is obvious from the pictures that the combined shaded areas are much more than a complete whole.

There are several errors in the incorrect procedure just described. The most obvious is that the five smaller shaded bits in the diagram are not all the same size, and so simply counting a total of 5 pieces is not a correct reflection of the combined size of the two fractions. However, there is a way around this problem.

First, divide each of the quarters in the diagram for 3 / 4 into three smaller, equal-sized pieces:

In fact, this diagram is now illustrating both 3 / 4 as well as 9 / 12, because now the whole can also be viewed as being partitioned into 12 equal pieces, of which 9 are shaded.

Secondly, divide each of the thirds in the diagram for 2 / 3 into four smaller equal-sized pieces:

Again, this results in the whole being divided into twelve equal pieces of which eight are shaded.

But now, both diagrams have shaded pieces which are the same size! Each is 1 / 12 of the whole. When the total number of these equal-sized shaded pieces is tallied, we get

9 + 8 = 17

shaded pieces, each of size 1 / 12 of the whole. Thus, we apparently get that

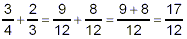
You can verify that this is a plausible result by using your calculator to turn the fractions into decimal numbers and checking the addition.

What this really shows is that we can add two fractions together only if they have the same denominator (and the same rule will apply to subtraction):

because for the sum of the numerators (or the difference of the numerators) to be meaningful, they must refer to pieces of the whole all of which are the same size (that is the same thing as saying that the denominators of the fractions are the same).