	Algebra Tutorials!

Saturday 21st of December



	Home
	Exponential Decay
	Negative Exponents
	Multiplying and Dividing Fractions 4
	Evaluating Expressions Involving Fractions
	The Cartesian Coordinate System
	Adding and Subtracting Fractions with Like Denominators
	Solving Absolute Value Inequalities
	Multiplying Special Polynomials
	FOIL Method
	Inequalities
	Solving Systems of Equations by Graphing
	Graphing Compound Inequalities
	Solving Quadratic Equations by Completing the Square
	Addition Property of Equality
	Square Roots
	Adding and Subtracting Fractions
	The Distance Formula
	Graphing Logarithmic Functions
	Fractions
	Dividing Mixed Numbers
	Evaluating Polynomials
	Power of a Product Property of Exponents
	Terminology of Algebraic Expressions
	Adding and Subtracting Rational Expressions with Identical Denominators
	Solving Exponential Equations
	Factoring The Difference of 2 Squares
	Changing Fractions to Decimals
	Solving Linear Equations
	Using Patterns to Multiply Two Binomials
	Completing the Square
	Roots of Complex Numbers
	Methods for Solving Quadratic Equations
	Conics in Standard Form
	Solving Quadratic Equations by Using the Quadratic Formula
	Simplifying Fractions 2
	Exponential Notation
	Exponential Growth
	The Cartesian Plane
	Graphing Linear Functions
	The Slope of a Line
	Finding Cube Roots of Large Numbers
	Rotating Axes
	Common Mistakes With Percents
	Solving an Equation That Contains a Square Root
	Rational Equations
	Properties of Common Logs
	Composition of Functions
	Using Percent Equations
	Solving Inequalities
	Properties of Exponents
	Graphing Quadratic Functions
	Factoring a Polynomial by Finding the GCF
	The Rectangular Coordinate System
	Adding and Subtracting Fractions
	Multiplying and Dividing Rational Expressions
	Improper Fractions and Mixed Numbers
	Properties of Exponents
	Complex Solutions of Quadratic Equations
	Solving Nonlinear Equations by Factoring
	Solving Quadratic Equations by Factoring
	Least Common Multiples
	http:
	Solving Exponential Equations
	Solving Linear Equations
	Multiplication Property of Equality
	Multiplying Mixed Numbers
	Multiplying Fractions
	Reducing a Rational Expression to Lowest Terms
	Literal Numbers
	Factoring Trinomials
	Logarithmic Functions
	Adding Fractions with Unlike Denominators
	Simplifying Square Roots
	Adding Fractions
	Equations Quadratic in Form
	Dividing Rational Expressions
	Slopes of Parallel Lines
	Simplifying Cube Roots That Contain Variables
	Functions and Graphs
	Complex Numbers
	Multiplying and Dividing Fractions 1
	Composition of Functions
	Intercepts of a Line
	Powers
	http:
	Multiplying Two Numbers with the same Tens Digit and whose Ones Digits add up to 10
	Factoring Trinomials
	Exponents and Polynomials
	Decimals and their Equivalent Fractions
	Negative Integer Exponents
	Adding and Subtracting Mixed Numbers
	Solving Quadratic Equations
	Theorem of Pythagoras
	Equations 1
	Subtracting Fractions
	Solving Quadratic Equations by Graphing
	Evaluating Polynomials
	Slope
	Angles and Degree Measure

Try the Free Math Solver or Scroll down to Tutorials!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

Solving Nonlinear Equations by Factoring

Solve for x: x⁴ - 21x² - 35 = 65

Example

Solution

Step 1 Write the equation in standard form.

Subtract 65 from both sides.

Step 2 Factor.

Step 3 Use the Zero Product Property.

Step 4 Solve for the variable.

x⁴ - 21x² - 35

x⁴ - 21x² - 100

(x² + 4)(x² - 25)

x² + 4 = 0 or x² -25

x² = - 4 or x²

= 65

= 0

= 25

So, there are four solutions: -2i, +2i, -5, and +5.

The equation x⁴ - 21x² - 35 = 65 written in standard form is x⁴ - 21x² - 100 = 0. The graph of the corresponding function, f(x) = x⁴ - 21x² - 100 is shown.

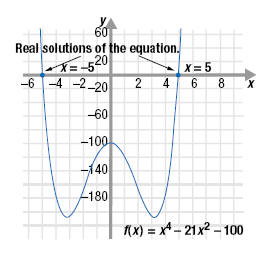
The graph crosses the x-axis at only two locations, x = -5 and x = 5. This is because these are the only real number solutions.