Solving Systems of Equations by Graphing
General Rules for Solving Systems Graphically:
Since solving systems graphically is not the easiest
method, the following outlines the Algebraic Methods for solving systems.
[Always solve algebraically first.]
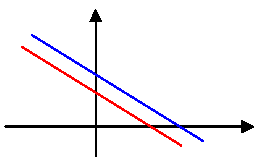
⇒ 1. If the lines are parallel. There is no solution. The system is inconsistent.
⇒ If two lines are parallel, their slopes are equal. m1 = m2
When solving the system by the algebraic Elimination Method
if the "letters" vanish and the resulting "sum" is not true, then
the two lines are likely parallel with no solution. Always check by
solving each equation for the form y = mx + b to see if the
slopes are equal.
Example 1:
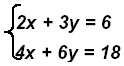
Multiply the first equation by − 2:
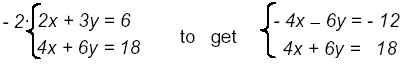
Add these equations
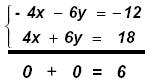 and note that
0 ≠ 6
Solve the equation: (1) 2x + 3y = 6 and find
 |
 |
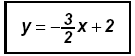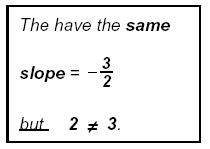Solve the equation: (2) 4x + 6y = 18 and find
 |
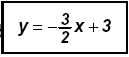Therefore the system is Parallel, no solution, inconsistent system.
⇒ 2. If the lines are coincident. There are infinite solutions The system is consistent.
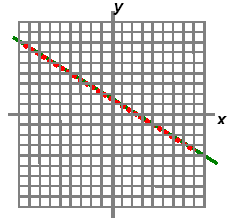
When solving the system by the algebraic Elimination Method
if the "letters" and the "numbers" vanish, which is true, then
the two lines are the same with infinite solutions. Always check by
solving each equation for the form y = mx + b to see if both
are the same equations.
Example 2:
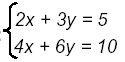
| Multiply equation (1) by -2:
|
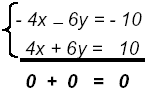(True) |
| Add the equations to get: |
Solve the equations:
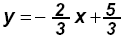 , Consistent system: Infinite solutions, Coincident (same line)
|
