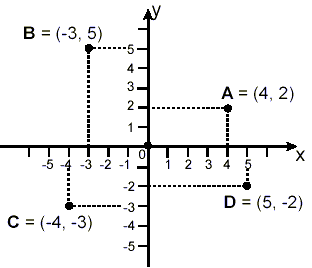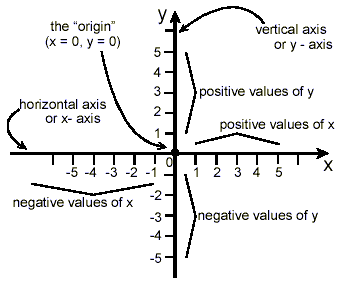
The Rectangular Coordinate System

When we write down a formula for some quantity, y, in terms of another quantity, x, we are expressing a relationship between the two quantities. For example, if we use the symbols

y = the area of a square

and

x = the length of one side of the square,

then the formula

y = x ²

tells us the relationship between the length of a side of a square and the area of the square. It tells us that to calculate the area of the square, we must raise the length of one side of that square to the power 2 (which is one reason why raising a number to the power 2 is often referred to as “squaring” the number).

We can use this formula to calculate the value of y for any particular value of x. This formula relating y to x is itself informative, but often we can understand the nature of the relationship between y and x even better if we have a visual image of its characteristics as well. This is where graphing formulas is helpful.

A graph of a relationship is a way of drawing points and other geometric shapes at locations representing the values of x and y. This is most commonly done using a so-called rectangular coordinate system . When the formula expresses y in terms of x, the coordinate system is usually arranged as:

• the vertical axis and the horizontal axis (often called the y-axis and the x-axis, respectively, if the two variables are y and x) intersect at a central point called the origin , which corresponds to y = 0 and x = 0. 1 2 3 4 5 -2 -3 -4 -5 1 2 3 4 5 -2 -1 -3 -4 -5 0 \fs34 y x horizontal axis or x- axis vertical axis or y - axis positive values of y positive values of x negative values of y negative values of x the “origin” (x = 0, y = 0)

• a numerical scale is created on each axis. Values on the horizontal axis increase from 0 at the origin though positive values to the right, and from 0 at the origin through negative values: -1, -2, -3, …, etc., to the left. The scales along the axes should be uniform – the values of x should be spaced uniformly along the length available.

• values on the vertical scale increase from 0 at the origin through positive values as you go upwards, and from 0 at the origin through negative values: -1, -2, -3, …, etc., as you go down.

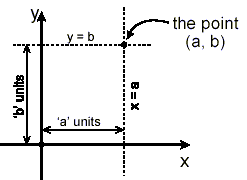
These two axes complete with the explicitly labelled numerical scales form what is called a rectangular coordinate system.

Then, the corresponding pair of values, x = a and y = b, written as a pair of numbers in this order in brackets, (a, b), corresponds to, or is plotted as a point at the location where the vertical line through x = a intersects the horizontal line through y = b:

The values x = a and y = b here are called the coordinates or rectangular coordinates of the point. You can also think of the coordinates, (a, b), of a point as indicating that to get to the point from the origin, you need to move ‘a’ units horizontally and ‘b’ units vertically. Positive movements are to the right horizontally, and upwards vertically. Negative movements are to the left horizontally and downwards vertically.

Example:

Plot the points

A = (4, 2)

B = (-3, 5)

C = (-4, -3)

and

D = (5, -2)

on the coordinate axes shown below.

Be sure to label the axes scales and label the points you plot.

Solution:

Recalling the meaning of this notation giving pairs of numbers in brackets, we know that the point A is the point that occurs at x = 4 and y = 2 – the first number in the brackets gives the xcoordinate of the point, and the second number in brackets gives the y-coordinate of the point.

Now, the x-coordinates for these four points range from a minimum of -4 to a maximum of 5, so our horizontal scales must go at least to -4 on the left to at least +5 on the right. Also, we see that the y-coordinates must go at least to -3 on the bottom to at least 5 on the top. The result is:

The dotted lines show how the points line up with the appropriate scale positions on both axes. Notice that the points are plotted as heavy dots – if you are just plotting points, there is no need to join them by lines or add any other features to the graph.