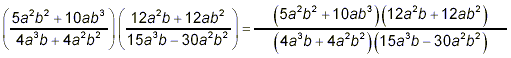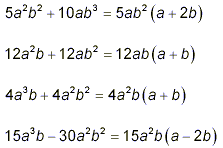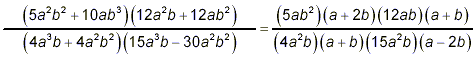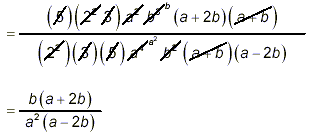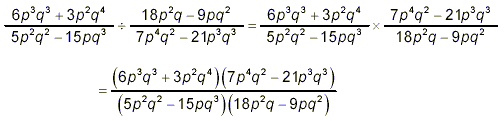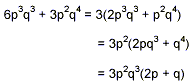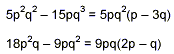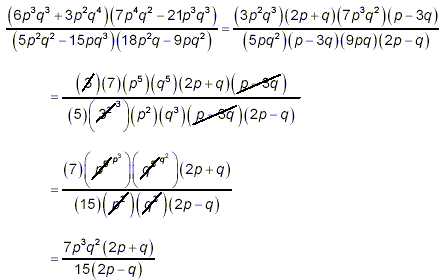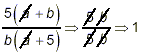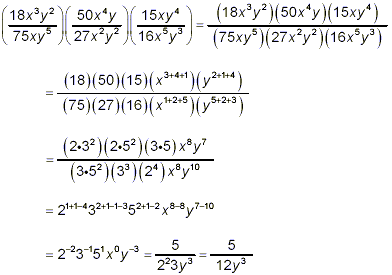Multiplying and Dividing Fractions

Examples with Solutions

Example 1:

Multiply and simplify the result.

solution: Although the expressions are rather more complicated here than in any previous examples, the same old strategy still applies. We need to simplify the product of the two fractions:

Even though the numerator and denominator here contain products of binomials, there is a temptation to multiply both of the products out separately. Here this would give us something like

which can be simplified, but surely has to look like we’re going in the wrong direction. Since simplifying fractions occurs via cancelling common factors between the numerator and the denominator, it is always far better to attempt more factorization than to consider multiplying to\par remove whatever factors are already present. So, we will abandon (at least for the present) continuing with this last monstrosity just above, and attempt to factor the original product. Considering existing factors one at a time, this turns out to be quite easy.

Thus

as our final answer. It is tempting to cancel the (a + 2b) in the numerator with the (a – 2b) in the denominator, but these two expressions are not identical, so it would be an error to cancel them. (If you enjoy a challenge, or if you are a glutton for punishment, you could attempt to simplify the gross “multiplied out” expression above. If you follow the strategies for factoring, it’s not impossible to do, and you will end up with the same final answer. Along the way, you may realize that some of the work you’re having to do is simply undoing the initial expansion operation – hence that initial step really was no progress at all!)

Example 2:

Simplify the result of dividing .

solution: The overall work to complete this problem is very similar to what appeared in the previous example, so you might try to do this one by yourself first, before looking at the solution to follow.

To avoid trying to do so many things at once that making errors becomes almost inevitable, we’ll do the factoring of each bracketed expression first. It’s probably prudent to do these factorizations in the step-wise fashion described earlier in these notes, since there is a fair amount of detail to keep track of here.

So

To save space, we’ll just list the final results of the factoring of the remaining three expressions:

So,

as the final result.

This problem, like the one in the previous example, looked horrible at a first glance. But you should spend enough time studying it step-by-step to see that as bad as it may look as a whole, the final result shows up almost automatically if you just carefully employ the basic strategy for simplifying fractions. Anyone can do the individual steps one-at-a-time required for solving this problem.

Example 3:

Simplify

solution: This looks too simple. We get

Even though there appears to be a lot of similar things in the numerator and denominator, no further cancellations are possible, and so this is the final answer. Probably most people would write it as

How do you know that, for example,

is wrong? Because in the first step, the a’s that are cancelled are not factors in either the numerator or the denominator. If what you’re cancelling are not common factors, then you’re making a mistake. The same applies here to suggestions that we cancel the b’s or the 5’s. In both cases, although one is a factor, the other is not, and so cancellation produces an invalid result. This is an example where, once we’ve done the initial division of one fraction by another, no further simplification of the result is possible.

Example 4:

Simplify:

solution: Although we’ve only looked at products of two factors so far, it is obvious that products of three or more fractions work the same way – just multiply the numerators together and multiply the denominators together, and then simplify the results. So here, we get

There was a lot of bookkeeping of factors here, so we took a few extra steps to ensure no errors were made. Recall that any number to the power zero just gives 1, and so x ⁰ = 1 in the last line above.

In a similar fashion, the rule for division can be extended to situations involving more than two fractions. However, in such cases, we would be dealing with some variation of a mixed multiplication and division problem. You should be able to sort such problems out if you pay careful attention to brackets or other symbols of grouping.