Factorials
Introduction
In many engineering calculations you will come across the
symbol ! which you may not have met before in mathematics
classes. This is known as a factorial. The factorial is a symbol
which is used when we wish to multiply consecutive whole numbers
together, as you will see below.
1. Factorials
The number 5×4×3×2×1 is written as 5!, which is read as
"five factorial". If you actually perform the
multiplication you will find that 5! = 120. Similarly 7! =
7×6×5×4×3×2×1 which equals 5040. A rather special case is
0!. This is defined to equal 1 and this might seem somewhat
strange. Just learn this!
You will not be required to find factorials of negative
numbers or fractions. Factorials are used in combination notation
which arises frequently in probability theory. The notation 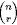 stands
for stands
for 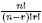 .
For example .
For example
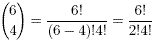
Exercises
1. Without using a calculator evaluate 2!, 3! and 4!.
2. Show that 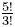 equals 20. equals 20.
3. Explain why n! = n×(n - 1)! for any positive whole number
n.
4. Explain why 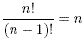 for any positive whole number n for any positive whole number n
5. Evaluate 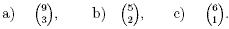
Answers
1. 2! = 2. 3! = 6 and 4! = 24. Note that 3! = 3×2!, and that
4! = 4×3!.
5. a) 84, b) 10, c) 6.
2. Using a calculator to find factorials
Your scientific calculator will be pre-programmed to find
factorials. Look for a button marked !, or consult your
calculator manual. Check that you can use your calculator to find
factorials by verifying that 10! = 3628800.
|