Finding Cube Roots of Large Numbers
The first thing you need to notice about cubed numbers is how
they are formed. For each digit in the number we are cubing,
three digits (at most) are formed for the product. We are going
to use this configuration to our advantage.
To find the cube root of a number mentally, use the following
steps:
Separate the number between the thousands digit and the
hundreds digit. The last digit of the number is an indicator of
the last digit of the cube root. The following chart gives the
last digit of each cube
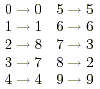
Notice that 0, 1, 4, 5, 6, and 9, when cubed has the same last
digit. Also notice that 2 switched with 8 and 3 switched with 7.
Using all the digits from the left to the thousands place (the
left part of the separation), take the cube root of the largest
cube less than this number as the digits on the left of the
answer.
Example:
Find the cube root of 79507.
First, separate the number into two parts, with the dividing
line between the thousands and the hundreds: 79 | 507. The number
that was cubed to get the ending 7 must have been 3. Therefore, 3
is the last digit of the cube root.
Next, look at the 79. The largest perfect cube less than 79 is
64. The cube root of 64 is 4. Thus, 4 is the first digit.
The cube root of 79507 is 43.
Example:
Find the cube root of 884,736. Separate the number into two
parts, 884 | 736. The number that was cubed to get the ending 6
must be 6. That makes the last digit of the cube root a 6.
Now, consider 884. The largest perfect cube less than 884 is
729. The cube root of 729 is 9 and that makes 9 is the first
digit of the cube root.
The cube root of 884,736 is 96.
Example:
Find the cube root of 1,481,544.
Even though there are seven-digits to this number, we still
separate the number between the thousands and the hundreds: 1481
| 544. The number that was cubed to get the end 4 must be 4 and
thus 4 is the last digit of the cube root.
The largest perfect cube less than 1481 is 1331 and the cube
root of 1331 is 11. Therefore, the first numbers must be 11.
The cube root of 1,481,544 is 114.
|