Reducing a Rational Expression to Lowest Terms
In each rational expression that follows, we will assume that no value of a
variable will make a denominator 0.
Like a fraction in arithmetic, a rational expression is usually easier to work
with when written in lowest terms.
The procedure for reducing a rational expression to lowest terms is like the
procedure for reducing a fraction to lowest terms.
Procedure —
To Reduce a Rational Expression to Lowest Terms
Step 1 Factor the numerator and denominator.
Step 2 Cancel all pairs of factors common to the numerator and
denominator.
Note:
When we have reduced a rational
expression to lowest terms, we also say we
have simplified the rational expression.
Here’s an example from arithmetic.
Reduce to lowest terms:
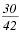
| Step 1 Factor the numerator and
denominator.
|
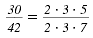 |
| Step 2 Cancel all pairs of factors common
to the numerator and denominator. |
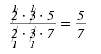 |
Thus,
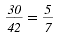
Remember, that w ≠ 0, x
≠ 0, and y ≠ 0.
We can also use the properties of
exponents to simplify this fraction:
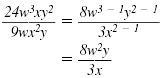
Example 1
Reduce to lowest terms:
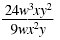
Solution
| Step 1
|
Factor the numerator
and denominator. |
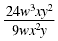 |
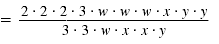 |
| Step 2 |
Cancel all pairs of
factors common to
the numerator and
denominator. |
|
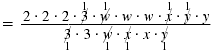 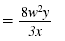 |
Thus,
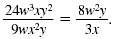
Example 2
Reduce to lowest terms:
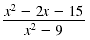
Note:
Remember, it is understood that x ≠ 3 and x
≠ -3.
Solution
Thus,
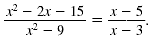
Note:
Like a fraction in arithmetic, a rational expression should normally be
written in lowest terms.
|