Exponents and Polynomials

Multiplication with Exponents

Definition of power: For n ∈ { natural numbers}, a > 0 and a ≠ 1,

a ⁿ = a · a · a · a ·...· a (n factors of a)

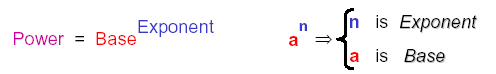
[NOTE: We also say "a to the n^th power"

Rule of signs: Remember (-1)(-1) = +1 and (-1)(-1)(-1) = - 1

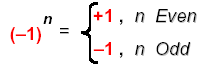
Generally, count the number of minus signs in a product. Attach "+" for even and "–" for odd

NOTE: The exponent affects only the number that it immediately touches so you must always put negative numbers in parentheses ( ).

Example 1:

1. 5³ = 5·5·5 = 125 base = 5, exponent = 3 Say "five to the third power"

2. –2⁴ = – 2·2·2·2 = – 16 base = 2, exponent = 4 "negative of two to the fourth power"

3. (- 2)⁴ = (-2)·(-2)·(-2)·(-2) = 16 base = -2, exponent = 4 "negative two to the fourth power"

4. 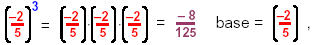exponent = 3 "negative two-fifths to the third power"

Multiplication of "powers with the same base"

Example 2:

1. 2⁴ ·2³ = ( 2·2·2·2 ) ×(2·2·2) = 2⁷ Notice that 4 + 3 = 7

2. (- 2)⁴·(- 2)³= [(-2)·(-2)·(-2)·(-2)] × [(-2)·(-2)·(-2)] = [16] ×[– 8] = – 128 = (- 2)⁷

1. For base a and m, n ∈ { natural numbers} → a^m ·aⁿ = a^{m + n}  → "Multiplication is short-cut addition" Add exponents.

Example 3:

1. 2⁵ ·2⁴ = 2⁹  = 512

2. x⁷ ·x⁹ = x¹⁶

Powering of "powers with the same base"

For base a and m, n ∈ { natural numbers} → (a^m)ⁿ = a^{m · n} → [Powering is short-cut multiplication – multiply exponents.]

Say: "To raise a power to a power, ^{multiply exponents}."

Example 4:

1. (2⁴ )³ = (2·2·2·2) ×(2·2·2·2) ×(2·2·2·2) = 2¹² Notice that 4 ×3 = 12

2. ((- 2)³) ³ = [(-2)·(-2)·(-2)] ×[(-2)·(-2)·(-2)] ×[(-2)·(-2)·(-2)]= (-2)⁹ = -2⁹ = - 512 [negative raised to an odd power] Notice that 3 ×3 = 9

Powering of "products with different bases"

For bases a and b, and n ∈ { natural numbers} → (a·b)ⁿ = aⁿ ·bⁿ = → say “The power of product is the product of the powers.”

Example 5:

1. (2·3)³ = (2·3)×(2·3)×(2·3) = (2·2·2 ) ×(3·3·3) = (2³)(3³)

2. (-2·x²y³)⁴ = (-2)⁴·(x²)⁴(y³)⁴ = 16·(x^2×4)(y^3×4) = 16 ·x⁸ ·y¹²